Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Numpy
- subplot
- linalg
- Operation function
- pivot table
- groupby
- Python 유래
- BOXPLOT
- VSCode
- namedtuple
- 정규분포 MLE
- seaborn
- boolean & fancy index
- 가능도
- python 문법
- 표집분포
- 딥러닝
- Numpy data I/O
- scatter
- 부스트캠프 AI테크
- type hints
- Python 특징
- Comparisons
- unstack
- Array operations
- Python
- ndarray
- 최대가능도 추정법
- dtype
- 카테고리분포 MLE
Archives
- Today
- Total
또르르's 개발 Story
[Stage 3 - 논문 리뷰] Transformer-DST 논문 리뷰 본문
문제 정의
성능 높은 모델들에 대한 리뷰
해결 아이디어
논문 : https://arxiv.org/abs/2010.14061
진행 상황
1. Key Idea
- 이전 논문들에서는 Encoder에서 BERT를 사용하지만, Value Generation부분에서는 RNN Decoder를 사용하는 아이러니..
- Purely Transformer-based framework를 사용 즉, Single BERT가 Encoder와 Decoder 모두에서 work → 이렇게 하면 prediction objective와 value generation objective가 BERT 하나만 optimize하게 됨
- Encoder(BERT)에서 사용한 hidden states 값을 Decoder(BERT)에서 Re-use가 가능해짐
2. Input
- Input으로는 SOM-DST와 같은 구조를 지님
- 아래 그림과 같이 D1, D2, S1을 INPUT으로 넣고, OUTPUT으로 S2를 출력

- $D_{t-1}, D_{t}, S_{t-1}$을 INPUT으로 $S_{t}$를 PREDICT
- $D_{t}$ : t번째 dialogue turn의 (System utterance, User response) pair
- $S_{t}$ : $(d_{j}, s_{j}, v_{j}) | 1<=j<=J$
여기서 $d$는 domain, $s$는 slot, $v$는 value를 나타냄
만약, 아무 정보도 없을시 $(d_{j}, s_{j})$로 나타내고, $v_{j}$는 NULL
3. Overview
- 왼쪽은 Transformer Encoder, 오른쪽은 Transformer Decoder
- Encoder (왼쪽)에서 $h_{sl}^{L}$ (hidden state)를 뽑아내고, Decoder (오른쪽)에서 Re-use하는 방법으로 사용됨
- Decoder (오른쪽)은 left-to-right attention (왼쪽에서 오른쪽으로 차례로 출력하는 language model, 즉 왼쪽 출력값이 오른쪽 입력)

4. Encoder
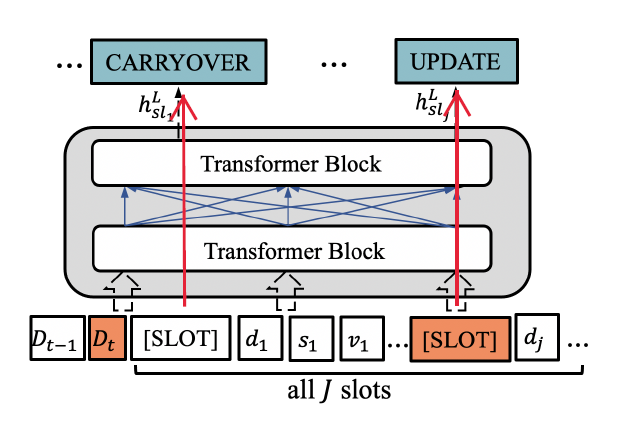
- Encoder의 Input은 $D_{t-1}, D_{t}, S_{t-1}$ 3가지가 들어감
- $D_{t}$는 t번째 turn의 ( System Utterance, User Resposne ) pair
- $S_{t-1}$은 $(d_{j}, s_{j}, v_{j}) | 1<= j <= J$
4-1) Encoder Input

- $[SLOT] \bigoplus d_{j} \bigoplus - \bigoplus s_{j} \bigoplus - \bigoplus v_{j}$ 으로 구성
- $\bigoplus$는 concat을 나타냄
- 총 $J$개의 domain-slot에 대해서 만들어줌
- $[SLOT] \bigoplus d_{j} \bigoplus - \bigoplus s_{j} \bigoplus - \bigoplus v_{j}$ * J번
- $[SLOT]$은 Transformer block을 통과한 후, $X^{l}{sl{j}}$ 형태로 출력되며, Prediction (CARRYOVER, ..., UPDATE 등)으로 사용됨
4-2) Multi-head self-attention

- Multi-head Self-attention 매카니즘 사용

- 여기서 $M^{x}$ : self-attention mask matrix
- $M^{x} \in R^{|x| \times |x|}$
- $M^{x}_{ij} \in \{0, - \infty \}$
- $M^{x}_{ij} = 0$이면 i-th position이 j-th position에 attend하다는 의미
- $M^{x}_{ij} = -\infty$이면 i-th position과 j-th position을 prevents하겠다는 의미
4-3) Encoder Output
$$X^{L} = [x^{L}{cls}, x^{L}{1}, ..., x^L_{sl_{1}}, ..., x^{L}{sl{J}},...]$$
4-4) Encoder Objective
- Encoder outputs $x^{L}{sl{j}}$에서 $[SLOT]$칸에 해당하는 값을 확인
- CARRYOVER, DELETE, DONTCARE, UPDATE
- UPDATE의 경우에만 decoder generater에서 사용함
5. Decoder (Slot Value Generation)
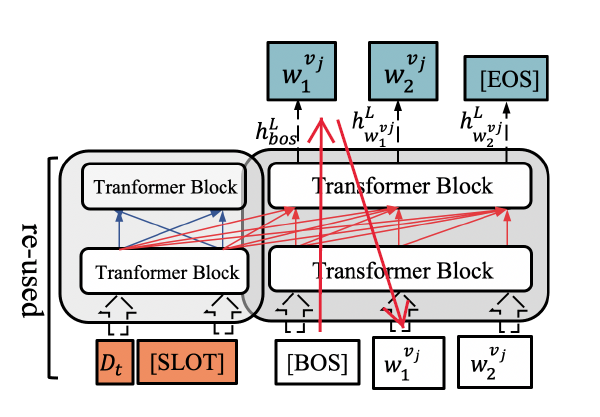
- Left-to-right self-attention을 사용함
- Encoder에서 도출해낸 hidden states를 decoder에서 reuse
- Resue의 의미는 hidden state를 decoder에서 다시 한번 계산할 필요가 없어진다는 의미를 갖음.
5-1) Decoder Input

- Encoder (reuse)
- 왼쪽의 $D_{t}$와 $[SLOT]$은 Encoder 부분을 나타냄
- 현재 turn의 $D_{t}$의 hidden state vector를 사용함
- $[SLOT]$ 중 UPDATE로 prediction이 된 hidden state vector만 사용함
- Decoder
- $[BOS]$는 String의 시작
- $w^{v_{j}}1, w^{v{j}}_2$는 decoder의 output을 다시 input으로 가지고 와서 사용 (left-to-right self-attention)
5-2) Left-to-right self-attention


- 일반 Multi-head attention하고 비슷
- $\hat{X}$ : re-used된 encoder hidden states
- $Y$ : Decoder hidden states
- $\hat{X}$와 $Y$를 concat해서 사용
- 만약 $j \leq i$일때, $M^{y}_{ij} = 0$ 으로 사용 (left-to-right attention)
5-3) Decoder Objective
- Generated slot value loss와 ground-truth slot value를 비교해서 Loss를 산출
- Teacher Forcing을 모든 time에서 사용
결과
- MutliWOZ 2.0과 MultiWOZ 2.1에서 제출 당시 SOTA

- 각각의 Domain의 Joint goal Accuracy를 비교
- 신기한 점은 Taxi 빼고 (다른 모델보다) 높은 성능을 보임
- 이유를 찾아보니 Taxi의 경우 Train과의 co-occurrence relations가 있음
- 하지만 Ours에는 이러한 점을 해결하려고 하지는 않았음

- 시간의 경우 SOM-DST보다는 Inference time이 오래걸림

- Reuse를 사용했을 경우에도 여러가지 방법을 시도해보았고, $D_{t} + [SLOT]$을 사용했을 때 Joint Accuracy에서 좋은 성능을 보였음

Reference
'[P Stage 3] DST > 논문리뷰' 카테고리의 다른 글
| [Stage 3 - 논문 리뷰] CHAN-DST 논문 리뷰 (0) | 2021.05.20 |
|---|---|
| [Stage 3 - 논문 리뷰] SOM-DST 논문 리뷰 (0) | 2021.05.20 |
| [Stage 3 - 논문 리뷰] TRADE 논문 리뷰 (0) | 2021.05.20 |
Comments



