[38-1] 경량화(1) - Pruning

1️⃣ Pruning

1) Weighted sum

Weighted sum은 가중해서 sum을 한다는 의미입니다.

 

결정 이론에서 "중요도가 있는 것"은 "높은 가중(weight)"을 곱하고, "중요도가 낮은 것"은 "낮은 가중(weight)"을 곱해서 어떤 부분에 중점을 두어야 하는지를 알려줍니다.

 

$$S = \sum_{i}^{N} w_{i}x_{i}$$

 

 

2) Pruning

"자주 사용하는 node" 또는 "중요한 node"는 놔두고, "자주 사용하지 않는 node"나 "중요하지 않는 node"는 pruning(가지치기)를 통해 없애주는 기법입니다.

 

Prunning을 하면 얻는 점과 잃는 점이 존재합니다.

 

얻는 점

- Inference speed (속도)

- Regularization (lessen model complexity) brings generalization (정규화)

 

잃는 점

- Information loss (정보)

- The granularity affects the efficiency of hardware accelerator design (디자인)

 

 

https://medium.com/@souvik.paul01/pruning-in-deep-learning-models-1067a19acd89

 

 

3) Deep Learning에서의 Pruning

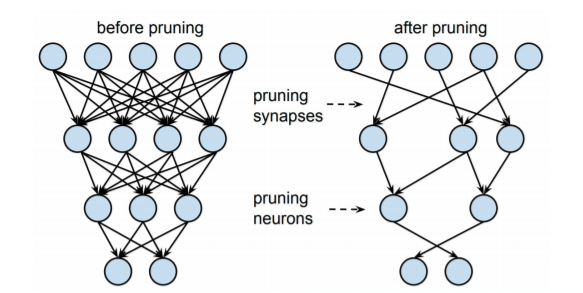
Deeop Learning에서의 pruning은 화살표로 표시되어있는 weight들을 잘라내서 만들게 됩니다.

 

아래 사진은 before pruning과 after pruning의 Weight distriubtion을 나타낸 것입니다.

 

Weight distribution은

Before pruning일 때는 0 주변에 분포되어 있었지만,

After pruning일 때는 0 부분이 움푹 꺼진 모양으로 들어가 있습니다. 대신 옆으로 퍼진 것을 알 수 있습니다.(x축의 범위가 다름; -0.02 ~ 0.02로 before pruning보다 퍼짐)

 

After pruning의 0 부분이 움푹 꺼진 모양을 하고 있는 이유는 0 주변의 weight 값들이 결과값에 영향을 거의 끼치지 않는다는 뜻입니다.

 

[Han. Song. et al., 2015]

 

2️⃣ Pruning vs Dropout

 

Pruning과 Dropout의 공통점과 차이점을 나누면 다음과 같습니다.

 

공통점

- 중간의 weight들을 끄고, 켜고 할 수 있습니다.

- Regularization을 위해 사용합니다.

 

차이점

- Pruning은 한 번 잘라낸 weight를 복원하지 않지만, Dropout은 weight들을 끄고, 켜고를 할 수 있으며 inference 할 때는 모든 네트워크를 켜서 사용합니다.

 

 

[Hinton et al., arXiv 2015]

 

Dropout과 Pruning에 대해 자세히 알아보면 다음과 같습니다.

 

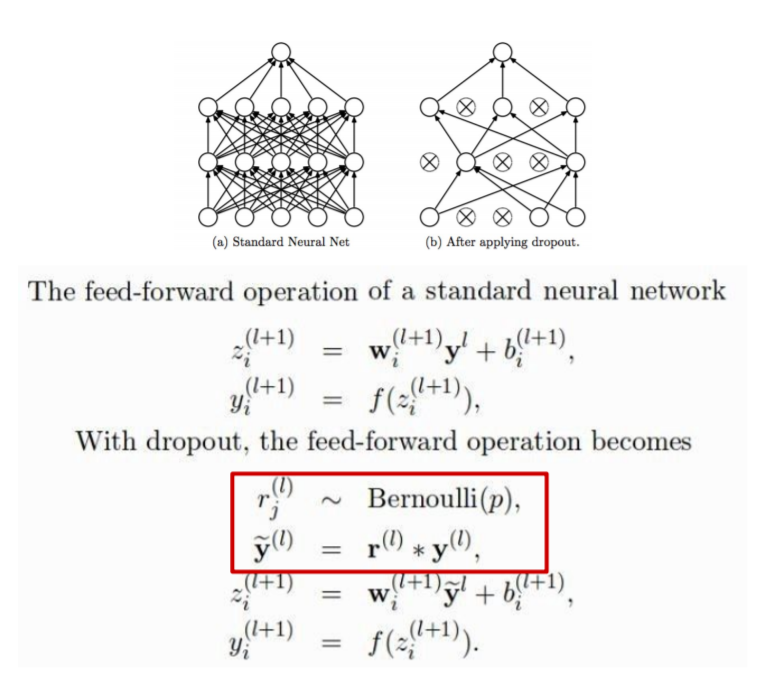
1) Dropout

Dropout은 앙상블 효과를 내기도 합니다. (하나를 끄고 켤 때마다 서로 다른 네트워크처럼 동작하기 때문에)

 

https://deepestdocs.readthedocs.io/en/latest/004_deep_learning_part_2/0042/

 

Dropout은 다음과 같은 방식으로 동작합니다.

 

[Blalock et al., arXiv 2020]

 

2) Pruning

Pruning의 경우에는 다음 순서로 동작합니다.

 

1. neuron의 importance를 측정합니다.
   
   
2. least important neuron을 제거합니다.
   
   
3. neruon이 제거된 network를 가지고 fine-tuning 합니다.
   
   
4. pruning을 다시 수행하던지, 아니면 종료합니다.

 

[Molchanov et al., arXiv 2016]

 

Pruning의 Alogorithm은 다음과 같습니다.

 

• W : Weight들의 set
  
  
• M : W 크기만큼의 1로 가득 차 있는 tensor (Mask)

 

[Blalock et al., arXiv 2020]

 

 

3️⃣ Pruning 비율에 따른 모델의 Accuarcy와 Loss

 

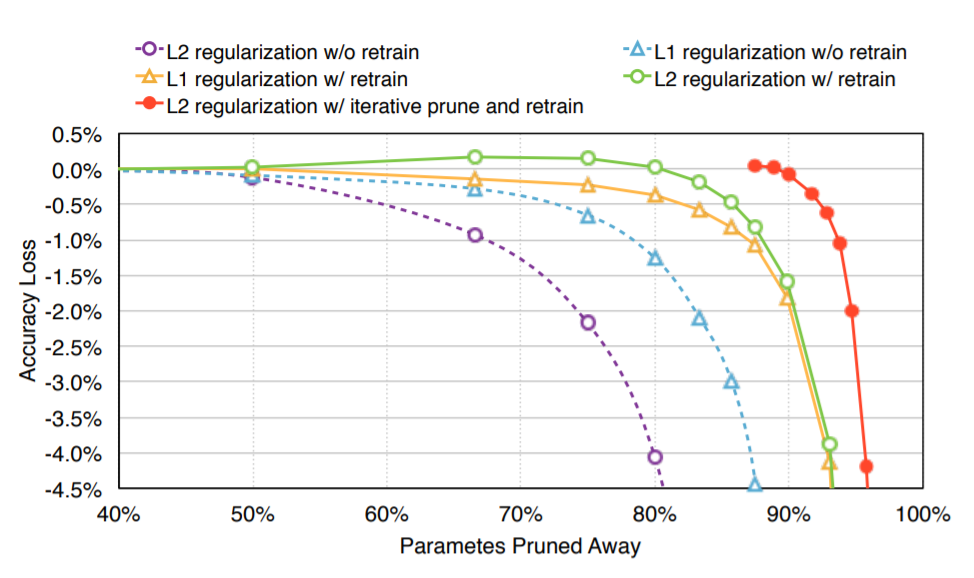
L1, L2 norm으로 정규화한 Pruning 비율에 따른 모델의 accuracy와 loss를 비교한 도표입니다.

 

retrain 없는 L2 regularization (보라색)을 했을 때 성능이 좋지 않지만,

retrain과 prune을 L2 regularization (빨간색)을 했을 때는 성능이 많이 올라갑니다.

 

즉, Iterative prune과 retrain을 하는 것이 성능 향상으로 이어집니다.

 

[Han et al., arXiv 2015]

 

 

4️⃣ 여러 Pruning 방법들

 

Pruning 방법에는 정말 정말 다양합니다.

다양한 pruning 방법들은 아래 github에서 확인할 수 있습니다.

he-y/Awesome-Pruning

https://github.com/he-y/Awesome-Pruning

 

이렇게 많은 Pruning을 category로 묶으면 다음과 같습니다.

 

[Blalock et al., arXiv 2020]

https://towardsdatascience.com/the-lottery-ticket-hypothesis-a-survey-d1f0f62f8884

 

1) Unstructured Pruning & Structured Pruning

• Unstructured Pruning : weight를 아무 규격 없이 잘라내는 pruning
  
  
• Structured Pruning : weight를 channel / layer 단위로 규격을 잡아 제거하는 pruning
  
  규격을 잡아 제거했기 때문에 hardward optimization이 잘 되는 경향이 있습니다.

 

https://deepai.org/publication/non-structured-dnn-weight-pruning-considered-harmful

 

아래 그림은 Unstructured Pruning과 Structured Pruning을 각각 수행한 Model들의 Weight distribution입니다.

(Weight distribution이 x축은 각 weight들이 가지고 있는 값 (-0.2, 0.12, 0, 1.1 등), y축은 모든 weight들의 각각의 값을 count 한 분포)

 

weight value가 0에 많다는 의미는 "중요하지 않은 weight들"이 몰려있다는 의미입니다.

따라서 weight에서 pruning을 하면 0에 가까운 값들이 제거됩니다.

 

[Liu et al., arXiv 2018]

 

여기서 "Pruning을 수행한 Fine-tuned와 Scratch-training"은 "Unpruned model"과 비교되는 부분은 다음과 같습니다.

바로 0에 가까운 weight value가 적어졌다는 것입니다.

이 것은 pruning을 수행한 architecture에서 0에 가까운 weight들에서 중복된 구조(redundant sturctures)를 많이 찾았다는 의미입니다.

 

또한, unstructured prunning에서 fine-tuned와 scratch training의 weight distribution이 많이 다르게 나왔다는 것을 알 수 있습니다. fine-tuned의 weight distribution에는 0 부분이 비어져 있습니다. 이 부분 때문에 "scratch training 된 모델"이 "fine-tuned 모델"의 accuracy를 따라잡을 수 없습니다.

 

 

 

2) Iterative pruning

Pruning을 한 번만 수행하고 종료하는 것이 아니라 Iterative (반복적)으로 수행합니다.

Pruning을 한 번에 많이 수행하게 되면, 많은 weight가 사라지게 되어pruning loss가 줄어든 후 Accuracy가 다시 올라가지 않는다고 알려져 있습니다.

 

그래서 pruning loss -> retraining -> pruning loss -> retraining ...을 반복적으로 수행합니다.

 

https://www.xilinx.com/html_docs/vitis_ai/1_2/pruning.html

 

Iterative Pruning의 algorithm은 다음과 같습니다.

 

[John et al. PMLR 2020]

 

 

5️⃣ Lottery Ticket Hypothesis

 

Lottery Ticket Hypothesis의 정의는 다음과 같습니다.

The Lottery Ticket Hypothesis. A randomly-initialized, dense neural network contains a subnetwork that is initialized such that—when trained in isolation—it can match the test accuracy of the original network after training for at most the same number of iterations

[Frankle et al., arXiv 2018]

 

정리해보면 다음과 같습니다.

 

Random으로 초기화된, dense 한 neural network는 subnetwork가 존재합니다. 만약, 그 subnetwork가 독립적으로 train 된다면, pruning 하기 전 얻었던 Accuracy (91%)를 pruning 하고 나서도 얻을 수 있는 subnetwork가 원래 network 안에 존재할 것이다라는 가설입니다.

 

https://medium.com/analytics-vidhya/rigging-the-lottery-training-method-of-high-speed-and-high-precision-sparse-networks-without-2340b0461d55

 

이 가설에는 subnetwork가 original network보다 epoch을 덜 돌면서, accuracy가 같거나 높고, parameter 수가 더 적을 것이라고 적어놓았습니다.

 

하지만 중요한 것은 original network를 reuse(재사용)해야 한다는 점입니다.

orignal network를 reuse하지 않고 subnetwork를 initialization을 새로해서 train 시키면 lottery ticket 효과가 사라지게 됩니다. 즉, original network의 initialization 된 parameter를 그대로 사용해야 Accuracy가 잘 나오는 subnetwork가 나오게 됩니다.

 

그렇기 때문에 이 논문의 한계점은 subnetwork를 찾기 위해서는 어쨌든 original network를 train 해서 찾아야 한다는 것입니다. original network를 훈련시키고 subnetwork를 다시 찾아야 하기 때문에 더 많은 cost를 소요하게 됩니다.

 

 

 

이러한 한계점을 극복하기 위해 차후에 나온 논문들입니다.

1) Iterative Magnitude pruning

Tickets을 찾기 위해 Iterative Magnitude pruning을 수행합니다.

(여기서 magnitude는 weight의 크기 기준으로 정렬해서 크기가 낮은 기준으로 잘라낸다는 의미)

 

init -> train -> prune -> mask를 씌우고 구조만 가지고 옴 (다른 내용은 remove) -> 다시 init 형태로 수행합니다.

 

 

2) Iterative Magnitude Pruning with Rewinding

여기서 rewinding은 되돌리다, 되감기를 의미합니다.

 

init -> train -> k 번째까지 iter 하고 weight를 저장 -> 다시 train -> prune -> 저장해놓은 k번째 weight을 모델에 덮어 씌운 후 iter 시작합니다.

 

 

이렇게 사용하면 cost를 절감해서 사용할 수 있습니다.

 

Weight rewinding을 Algorithm으로 표현하면 다음과 같습니다.

• $u$ : noise
• $m \odot W_{k}$ : $W_{k}$에 마스크를 씌움

[Frankle et al., PMLR 2020]

 

아래 그림을 가지고 설명하면 다음과 같습니다.

 

랜덤하게 initalization 된 $W_{0}$에서 $k$번째까지 iteration을 수행하면 $W_{k}$가 나오게 됩니다.

이때, 약간의 noise를 집어넣고서 $W^{1}_{T}$와 $W^{2}_{T}$ 등 여러 방향으로 train 시킵니다. (똑같은 방향으로 train 시키면 rewind 의미가 없어짐)

 

[Frankle et al., PMLR 2020]