Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- type hints
- Comparisons
- 표집분포
- Numpy data I/O
- groupby
- 가능도
- Python 특징
- scatter
- ndarray
- Array operations
- seaborn
- 딥러닝
- dtype
- linalg
- Python
- 정규분포 MLE
- Python 유래
- unstack
- 부스트캠프 AI테크
- pivot table
- Operation function
- python 문법
- Numpy
- boolean & fancy index
- BOXPLOT
- VSCode
- 최대가능도 추정법
- namedtuple
- subplot
- 카테고리분포 MLE
Archives
- Today
- Total
또르르's 개발 Story
[14-3] Scaled Dot-Product Attention (SDPA) using PyTorch 본문
부스트캠프 AI 테크 U stage/실습
[14-3] Scaled Dot-Product Attention (SDPA) using PyTorch
또르르21 2021. 2. 4. 23:55Transformer에서 가장 중요하게 여겨지는 부분은 Self-Attention 구조입니다.
Self-Attention에서 사용되는 방법 중 하나인 Scaled Dot-Product Attention (SDPA)의 코드 구현입니다.
Self-Attention에서 차원이 어떻게 바뀌는지를 최대한 정리해보았습니다.
1️⃣ 설정
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
%matplotlib inline
%config InlineBackend.figure_format='retina'
print ("PyTorch version:[%s]."%(torch.__version__))
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print ("device:[%s]."%(device))
2️⃣ Scaled Dot-Product Attention (SDPA)
Attention의 Q (Query vector), K (Key vector), V (value vector)는 아래와 같은 상관관계를 가지게 됩니ㅏㄷ.
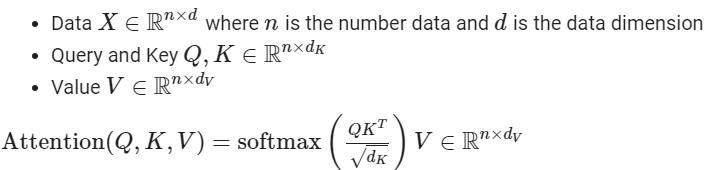
위 $Attention(Q,K,V)$식을 코드로 구현하면 아래와 같습니다.
class ScaledDotProductAttention(nn.Module):
def forward(self,Q,K,V,mask=None): # query, key, value가 들어오게되면
d_K = K.size()[-1] # key dimension을 찾고
scores = Q.matmul(K.transpose(-2,-1)) / np.sqrt(d_K) # scores value
if mask is not None: # mask가 없다고 가정
scores = scores.masked_fill(mask==0, -1e9)
attention = F.softmax(scores,dim=-1)
out = attention.matmul(V) # attention * value = out vector
return out,attentionSPDA를 수행하면 아래와 같은 dimensions가 나오게됩니다.
# Demo run of scaled dot product attention
SPDA = ScaledDotProductAttention()
# n_batch는 3개의 input (3개의 단어)
# key의 dimension과 value의 dimension은 달라도 되지만 되도록이면 같게 (여기서는 달라도 동작한다는 것을 보여줌)
n_batch,d_K,d_V = 3,128,256 # d_K(=d_Q) does not necessarily be equal to d_V
# Q,K,V의 개수
n_Q,n_K,n_V = 30,50,50
# Q의 개수 != K의 개수 = V의 개수
# 왜냐면 Q는 decoder에서 나오고, K,V는 encoder 최상위 layer에서 나옴
Q = torch.rand(n_batch,n_Q,d_K)
K = torch.rand(n_batch,n_K,d_K)
V = torch.rand(n_batch,n_V,d_V)
out,attention = SPDA.forward(Q,K,V,mask=None)
def sh(x): return str(x.shape)[11:-1]
print ("SDPA: Q%s K%s V%s => out%s attention%s"%
(sh(Q),sh(K),sh(V),sh(out),sh(attention)))SDPA: Q[3, 30, 128] K[3, 50, 128] V[3, 50, 256] => out[3, 30, 256] attention[3, 30, 50]
# out은 query의 개수(30)에 대해서 나옴위의 SDPA를 가지고도 Multi-Headed Attention에도 사용이 가능합니다.
Q,K,V에 각각 n_head가 들어가 있는데 두 번째에 n_head dimension이 들어가도 사용이 가능합니다.
# It supports 'multi-headed' attention
n_batch,n_head,d_K,d_V = 3,5,128,256
n_Q,n_K,n_V = 30,50,50 # n_K and n_V should be the same
Q = torch.rand(n_batch,n_head,n_Q,d_K)
K = torch.rand(n_batch,n_head,n_K,d_K)
V = torch.rand(n_batch,n_head,n_V,d_V)
out,attention = SPDA.forward(Q,K,V,mask=None)
# out: [n_batch x n_head x n_Q x d_V]
# attention: [n_batch x n_head x n_Q x n_K]
def sh(x): return str(x.shape)[11:-1]
print ("(Multi-Headed) SDPA: Q%s K%s V%s => out%s attention%s"%
(sh(Q),sh(K),sh(V),sh(out),sh(attention)))(Multi-Headed) SDPA: Q[3, 5, 30, 128] K[3, 5, 50, 128] V[3, 5, 50, 256] => out[3, 5, 30, 256] attention[3, 5, 30, 50]위 코드를 그대로 사용해도 되지만, Multi-Headed Attention을 다시 새로 작성하겠습니다.
3️⃣ Multi-Headed Attention
1) Multi-Headed Attention
class MultiHeadedAttention(nn.Module):
# d_feat => feature dimension, n_head => head 개수, dropout => attention rate에 들어감
def __init__(self,d_feat=128,n_head=5,actv=F.relu,USE_BIAS=True,dropout_p=0.1,device=None):
"""
:param d_feat: feature dimension
:param n_head: number of heads
:param actv: activation after each linear layer
:param USE_BIAS: whether to use bias
:param dropout_p: dropout rate
:device: which device to use (e.g., cuda:0)
"""
super(MultiHeadedAttention,self).__init__()
if (d_feat%n_head) != 0: # feature dimension이 head의 개수로 나눠줄 것
raise ValueError("d_feat(%d) should be divisible by b_head(%d)"%(d_feat,n_head))
self.d_feat = d_feat
self.n_head = n_head
self.d_head = self.d_feat // self.n_head
self.actv = actv
self.USE_BIAS = USE_BIAS
self.dropout_p = dropout_p # prob. of zeroed
# 임의의 embedding vector가 들어왔을 때, query, key, value 벡터를 얻어내는 네트워크
# 그리고 lin_O에서 나온 것을 추가로 한 번 더 가공
self.lin_Q = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
self.lin_K = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
self.lin_V = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
self.lin_O = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
self.dropout = nn.Dropout(p=self.dropout_p)
def forward(self,Q,K,V,mask=None):
"""
:param Q: [n_batch, n_Q, d_feat]
:param K: [n_batch, n_K, d_feat]
:param V: [n_batch, n_V, d_feat] <= n_K and n_V must be the same
:param mask:
"""
# Q,K,V가 들어오면 한 번씩 Linear을 거침
n_batch = Q.shape[0]
Q_feat = self.lin_Q(Q)
K_feat = self.lin_K(K)
V_feat = self.lin_V(V)
# Q_feat: [n_batch, n_Q, d_feat]
# K_feat: [n_batch, n_K, d_feat]
# V_feat: [n_batch, n_V, d_feat]
# Multi-head split of Q, K, and V (d_feat = n_head*d_head)
# 나온 feature을 조각조각 내줌 (논문하고 다름)
Q_split = Q_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
K_split = K_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
V_split = V_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
# Q_feat와 Q_split의 다른점은 d_feat에서 n_head와 d_head로 나눠진 점 (나머지도 마찬가지)
# d_feat = 100개면 n_head=10개, d_head=10개 이런식으로
# Q_split: [n_batch, n_head, n_Q, d_head]
# K_split: [n_batch, n_head, n_K, d_head]
# V_split: [n_batch, n_head, n_V, d_head]
# Multi-Headed Attention
d_K = K.size()[-1] # key dimension
# permute는 transpose같은 느낌, permute할 떄는 K_split의 dimension 확인
scores = torch.matmul(Q_split, K_split.permute(0,1,3,2)) / np.sqrt(d_K)
if mask is not None:
scores = scores.masked_fill(mask==0,-1e9)
attention = torch.softmax(scores,dim=-1)
x_raw = torch.matmul(self.dropout(attention),V_split) # dropout is NOT mentioned in the paper
# attention: [n_batch, n_head, n_Q, n_K]
# x_raw: [n_batch, n_head, n_Q, d_head]
# Reshape
# reshape을 해주는 이유는 뒤쪽에서 Linear layer를 할 때 batch the multiplication을 하기 위해
# 4차원 rank -> 3차원 rank로 변경
x_rsh1 = x_raw.permute(0,2,1,3).contiguous()
# x_rsh1: [n_batch, n_Q, n_head, d_head]
x_rsh2 = x_rsh1.view(n_batch,-1,self.d_feat)
# x_rsh2: [n_batch, n_Q, d_feat]
# Linear
x = self.lin_O(x_rsh2)
# x: [n_batch, n_Q, d_feat]
out = {'Q_feat':Q_feat,'K_feat':K_feat,'V_feat':V_feat,
'Q_split':Q_split,'K_split':K_split,'V_split':V_split,
'scores':scores,'attention':attention,
'x_raw':x_raw,'x_rsh1':x_rsh1,'x_rsh2':x_rsh2,'x':x}
return out
2) Init Attention
# Self-Attention Layer
n_batch = 128 # 128개의 데이터를 뜯어온 것, 데이터들은 independent
n_src = 32 # 32개의 word가 한 번에 들어가서 32개의 sequence 처리
d_feat = 200 # feature는 200차원
n_head = 5 # 5개의 attention
src = torch.rand(n_batch,n_src,d_feat)
self_attention = MultiHeadedAttention(
d_feat=d_feat,n_head=n_head,actv=F.relu,USE_BIAS=True,dropout_p=0.1,device=device)
out = self_attention.forward(src,src,src,mask=None) # Q,K,V 모두 self-attention을 사용하기 때문에 src가 3개에 들어감
Q_feat,K_feat,V_feat = out['Q_feat'],out['K_feat'],out['V_feat']
Q_split,K_split,V_split = out['Q_split'],out['K_split'],out['V_split']
scores,attention = out['scores'],out['attention']
x_raw,x_rsh1,x_rsh2,x = out['x_raw'],out['x_rsh1'],out['x_rsh2'],out['x']이 값들을 print하게 되면 아래와 같습니다.
# Print out shapes
def sh(_x): return str(_x.shape)[11:-1]
print ("Input src:\t%s \t= [n_batch, n_src, d_feat]"%(sh(src)))
print ()
print ("Q_feat: \t%s \t= [n_batch, n_src, d_feat]"%(sh(Q_feat)))
print ("K_feat: \t%s \t= [n_batch, n_src, d_feat]"%(sh(K_feat)))
print ("V_feat: \t%s \t= [n_batch, n_src, d_feat]"%(sh(V_feat)))
print ()
print ("Q_split: \t%s \t= [n_batch, n_head, n_src, d_head]"%(sh(Q_split)))
print ("K_split: \t%s \t= [n_batch, n_head, n_src, d_head]"%(sh(K_split)))
print ("V_split: \t%s \t= [n_batch, n_head, n_src, d_head]"%(sh(V_split)))
print ()
print ("scores: \t%s \t= [n_batch, n_head, n_src, n_src]"%(sh(scores)))
print ("attention:\t%s \t= [n_batch, n_head, n_src, n_src]"%(sh(attention)))
print ()
print ("x_raw: \t%s \t= [n_batch, n_head, n_src, d_head]"%(sh(x_raw)))
print ("x_rsh1: \t%s \t= [n_batch, n_src, n_head, d_head]"%(sh(x_rsh1)))
print ("x_rsh2: \t%s \t= [n_batch, n_src, d_feat]"%(sh(x_rsh2)))
print ()
print ("Output x: \t%s \t= [n_batch, n_src, d_feat]"%(sh(x)))Input src: [128, 32, 200] = [n_batch, n_src, d_feat] # 32길이의 다른 단어들이 128개 들어옴
Q_feat: [128, 32, 200] = [n_batch, n_src, d_feat] # 서로 다른 네트워크로 Q,K,V를 찾아주는 것
K_feat: [128, 32, 200] = [n_batch, n_src, d_feat]
V_feat: [128, 32, 200] = [n_batch, n_src, d_feat]
# multi-headed attention을 하기 위해서 d_feat=200차원을 가지고 5개의 n_head를 만드는 것이 아니라
# (아래와 같이) 40 dimension짜리의 작은 feature들을 가지고 multi-headed attention을 수행함
# Q_split, K_split, V_split은 shape만 바뀜
Q_split: [128, 5, 32, 40] = [n_batch, n_head, n_src, d_head]
K_split: [128, 5, 32, 40] = [n_batch, n_head, n_src, d_head]
V_split: [128, 5, 32, 40] = [n_batch, n_head, n_src, d_head]
# 5개의 head들은 40차원의 입력만을 받아서 independent하게 돌아감
scores: [128, 5, 32, 32] = [n_batch, n_head, n_src, n_src]
attention: [128, 5, 32, 32] = [n_batch, n_head, n_src, n_src]
x_raw: [128, 5, 32, 40] = [n_batch, n_head, n_src, d_head]
x_rsh1: [128, 32, 5, 40] = [n_batch, n_src, n_head, d_head]
# x_rsh2는 5개의 head들이 각각 독립적으로 40 dimension을 입력으로 받아 score를 수행하고 다시 concat해서 200 dimension으로 돌려줌
x_rsh2: [128, 32, 200] = [n_batch, n_src, d_feat]
# concat 시킨 값이라서 각각의 dimension에는 다른 값이 들어가 있음 => 다시 한 번 200 x 200 neural network를 만들어서 재처리해주면 output
Output x: [128, 32, 200] = [n_batch, n_src, d_feat]'부스트캠프 AI 테크 U stage > 실습' 카테고리의 다른 글
| [16-2] Word2Vec Using Konlpy (0) | 2021.02.16 |
|---|---|
| [16-1] NaiveBayes Classifier Using Konlpy (0) | 2021.02.16 |
| [14-2] LSTM using PyTorch (0) | 2021.02.04 |
| [13-3] Google Image Data 다운로드 (0) | 2021.02.04 |
| [13-2] Colab에서 DataSet 다루기 (강아지 DataSet) (0) | 2021.02.04 |
Comments



