| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- unstack
- 가능도
- groupby
- Python
- dtype
- seaborn
- 표집분포
- linalg
- Python 유래
- BOXPLOT
- type hints
- subplot
- Python 특징
- Numpy data I/O
- namedtuple
- 부스트캠프 AI테크
- python 문법
- pivot table
- boolean & fancy index
- VSCode
- 정규분포 MLE
- ndarray
- Comparisons
- Array operations
- Operation function
- 최대가능도 추정법
- Numpy
- 카테고리분포 MLE
- scatter
- 딥러닝
- Today
- Total
또르르's 개발 Story
[15] Generative Models 본문
Generative model 즉, 생성 모델은 주어진 학습데이터를 학습하여 학습데이터의 분포를 따르는 유사한 데이터를 생성하는 모델입니다.
학습 데이터와 유사한 샘플을 뽑아야 하기 때문에,
- 학습 데이터의 분포를 어느정도 안 상태에서 생성 (Explicit)
- 학습 데이터의 분포를 잘 모르지만 생성 (Implicit)
모델이 존재합니다.
생성모델에서의 중요한 점은 "학습 데이터의 분포 ~$P_{data}(x)$와의 차이"가 적을수록 실제 데이터와 비슷한 데이터를 생성할 수 있습니다.

아래 그림과 같이 Generative model은 다양합니다.

1️⃣ Tractable density
Tractable density는 Auto-regressive Model(자기 회귀 모델)을 사용합니다.
즉, 이전 픽셀들의 값을 통해서 현재 픽셀의 값을 결정하겠다는 것입니다.
이 방법은 Conditional Independence (조건부 독립)을 통해서 값을 구할 수 있습니다.
✅ Auto-regressive Model(자기 회귀 모델)
Auto-regressive는 어떤 하나의 정보가 이전 정보들에 dependent 한 것을 뜻합니다.
즉, 현재 정보를 결정하기 위해서 이전 정보를 활용하는 모델입니다.
$i$번째 모델이 $i-1$에 dependent한 것도 auto-regressive model이지만
$i$번째 모델이 $1,...,i-1$ 모델에 dependent한 것도 auto-regressive model을 뜻합니다.
이전 1개의 정보만 고려하는 모델은 $AR(1)$라고 쓰고, 이전 n개의 정보만 고려하는 모델은 $AR(n)$라고 씁니다.
따라서 auto-regressive model은 순서(ordering)가 중요해집니다.
순서(ordering)에 따라서 model의 확률분포가 완전히 달라질 수 있기 때문입니다.
Auto-regressive model은 다음과 같은 수식으로 표현됩니다.
여기서 $P(x)$는 $x$에 대한 가능도(Likelihood; 확률밀도함수에서 y값)를 나타냅니다.

위 수식은 연쇄법칙(Chain rule)을 활용해서 풀어야합니다.
- 연쇄 법칙 (Chain rule)
연쇄법칙은 베이즈 정리를 사용해서 $P(x_{1}, ..., x_{n})$를 표현이 가능합니다.

✅ 조건부 독립(Conditional Independence)
Auto-regressive model은 조건부 독립(Conditional Independence)을 사용해서 parameter 수를 줄일 수 있습니다.
만약, RGB 모델의 분포 (r,g,b) ~ $p(R, G, B)$는 아래와 같이 표현됩니다.

- R,G,B를 표현하는데 경우의 수는?
256 x 256 x 256
- R,G,B를 표현하는데 필요한 parameter의 수는?
255 x 255 x 255
(카테고리 분포에서 n개의 경우의 수가 있을 때, parameter는 n-1개만 있어도 됩니다. 왜냐하면, $\sum^{n}_{i=1}P_{i}=1$을 사용해서 1에서 다 빼주면 되기 때문)
하지만 확률변수 $x_{1}, ...., x{n}$가 independent 하다면 아래와 같이 표현이 가능합니다.
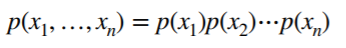
- $p(x_{1}, ..., x_{n})$을 표현하는데 경우의 수는?
$2^{n}$
- $2^{n}$가 모두 independence 하다면 $2^{n}$을 표현하는데 필요한 parameter의 수?
$n$
(왜냐하면 각각의 픽셀에 대해서 parameter가 1개만 있으면 됨, independence 하다면 각 픽셀 값을 다 더하면 되기 때문에)
위의 경우 같이 확률변수들이 모두 independent 하다면 parameter의 수를 많이 줄일 수 있습니다.
이와 같이, Auto-regressive model에서 연쇄 법칙(chain model)을 사용하면 parameter가 너무 많아지기 때문에연쇄 법칙(chain model)과 조건부 독립(Conditional Independence)을 적절히 배합해서 중간을 찾고자 합니다.
Fully dependent 하면 너무 많은 parameter가 존재하고, 너무 independent 하면 표현력이 작아지기 때문이죠.
조건부 독립(Conditional Independence)은 아래 수식처럼 표현됩니다.
여기서 $\perp$는 독립이라는 뜻입니다.
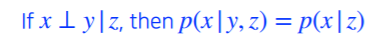
z가 주어졌을 때, x와 y가 independence 하다는 조건이 있다면,
x,y가 independece 하기 때문에 y가 상관이 없어집니다.
따라서, 연쇄 법칙(chain rule)에서

원래의 parameter의 개수는 아래와 같습니다.

하지만 이때, Markov 가정(Markov assumption) $X_{i+1} \perp X_{1}, ..., X_{i-1} | X_{i}$ 을 사용합니다.
(markov assumption은 $X_{i+1}$은 $X_{i}$에만 dependent 하고 나머지 $1, ...., X_{i-1]$에는 independent 하다고 가정)
parameter의 개수는 아래와 같습니다.
$$2n-1$$
이런 식으로 Auto-regressive model은 조건부 독립(conditional independency)을 활용하여 Parameter를 효율적으로 줄입니다.
1) NADE : Neural Autoregressive Density Estimator
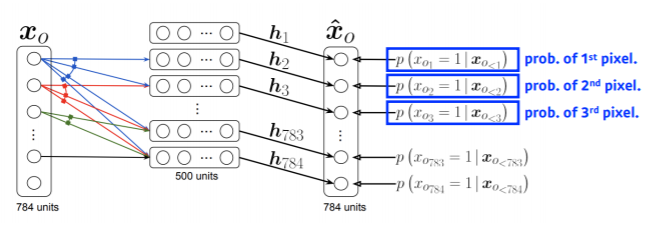
NADE는 연쇄 법칙 (chain rule)을 사용한 모델입니다.
첫 번째 pixel은 모든 pixel에 independent 하게,
두 번째 pixel은 첫 번째 pixel에만 dependent 하게,
세 번째 pixel은 첫 번째, 두 번째 pixel에만 dependent 하게,
i번쨰 pixel은 i-1개의 pixel에 dependent 하게 만듭니다.
이때, NADE는 depentdent 한 pixel들을 neural network에 넣어서 single scalar로 만든 다음, sigmoid를 통과해서 각 확률을 산출합니다.
이때, neural network는 입력 차원이 계속 달라지게 때문에(pixel 개수가 달라지기 때문) weight가 계속 증가하는 문제점이 존재합니다.
(예를 들어, 100번째 pixel을 할 때 99개의 neural network를 받을 수 있는 weight가 필요함)
NADE는 explict model입니다. (density가 가능하기 때문)
(논문에 density가 들어가 있으면 explic model일 확률이 높음)
2) Pixel RNN
Pixel RNN은 RNN을 사용한 auto-regressive model입니다.
예를 들어, n x n 크기의 RGB image가 input으로 들어오게 되면, 아래 수식을 통해 계산할 수 있습니다.

여기서 중요한 점은 순서(ordering)입니다. 순서에 따라 다른 값이 나올 수 있기 때문입니다.
Row LSTM은 i번째 pixel을 만들 때 위쪽에 있는 pixel들을 이용하는 것이고,
Diagonal BiLSTM은 i번째 pixel을 만들 때 자기 이전 pixel들을 모두 활용합니다.

2️⃣ Variantional Auto-encoder
Auto-encoder는 입력을 기반으로 특징을 추출하고, 추출된 특징으로 다시 원본 데이터를 출력하는 네트워크입니다.
따라서 Auto-encoder는 encoder, decoder 2가지로 구성되어 있습니다.
그렇다면 auto-encoder를 generative model라고 할 수 있을까요?
명확하게 말하면 auto-encoder는 generative model이 아닙니다.
auto-encoder는 라벨링 되지 않은 데이터로부터 Low-dimensional feature representation(저 차원 특징)을 학습한 비지도 학습이기 때문입니다. 여기서 encoder에서 추출된 feature을 Latent attributes(잠재 속성)라고 합니다.
1) Variantional Auto-encoder

-
Variational inference(VI)
Variational inference는 posterior distribution(사후 분포)을 찾아서 variantional distribution를 최적화하는 게 목적입니다.
- posterior distribution(사후 분포) $p_{\theta}(z|x)$ : 데이터$x$가 관찰되었을 때 내가 관심 있어하는 확률분포
- Variational distribution $q_{\phi}(z|x)$ : posterior distribution(사후분포)을 찾기 어렵기 때문에 최적화시킬 수 있는 값으로 근사하는 확률분포
따라서 Variational inference는 Variational distribution을 찾는 과정을 말하고, 이 것은 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)을 사용해서 Variational distribution와 posterior distribution과의 차이를 최소화하겠다는 것을 뜻합니다.

쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)에 대한 정리는 아래 링크에 있습니다.
[10-1] 딥러닝에 사용되는 통계학
딥러닝에서는 데이터를 받아들여 통계적 모델을 만들고 결과값을 추정합니다. 따라서 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표이며, 기계학습이 추구하는
dororo21.tistory.com
문제는 현실에서는 posterior distribution(사후분포)를 모를 때가 더 많다는 점입니다.
posterior distribution(사후분포)도 모르는데 그 값을 근사하는 Variational distribution는 찾는 것은 불가능한 일입니다.
-
ELBO
이것을 가능하게 해주는 것이 ELBO 수식입니다.
아래 수식은 $P_{\theta}(D)$를 구하는 과정에서 Variational distribution와 posterior distribution의 사이의 KL Divergence을 줄이는 것이 목적인데 이것이 불가능하기 때문에,

ELBO(Evidence Low Bound)라는 것을 계산한 후, ELBO를 키움으로써 반대로 원하는 objective(Variational distribution와 posterior distribution의 사이의 KL Divergence을 줄이는 것)를 얻고자 하는 것 (값은 정해져 있고, ELBO를 높이면 objective가 낮아짐)
ELBO 식을 나눠서 분석해보면 아래 수식과 같습니다.

ELBO를 활용해서 궁극적으로 하려는 것은
"$x$라는 입력에 대해서 그것을 잘 표현할 수 있는 latent space(잠재 공간)를 찾고 싶은 것"입니다.
- Reconstruction Term
encoder를 통해서 $x$라는 입력을 latent space로 보냈다가 다시 decoder로 돌아오는 reconstruction loss를 줄이는 term
- Prior Fitting Term
latent distrubution과 prior distribution과 비슷하게 만들어주는 term
-
Variantional Auto-encoder의 한계점
- Intractable model (다루기 힘든 모델) : likelihood(가능도) 측정이 어려움, explict model이 아님
- Prior Fitting Term은 무조건 미분이 가능해야 함 : KL divergence에 적분이 있기 때문에 미분이 가능해야 함. 그래서 대부분의 variantional encoder는 Gaussian prior을 사용합니다. 왜냐하면 Gaussian이 몇 안 되는 KL divergence가 closed-form(유한한 term을 가지고 표현할 수 있는 식)에 있는 분포이기 때문입니다.
- 일반적으로 isotropic Gaussian을 사용 : 모든 output dimension이 independent 한 gaussian
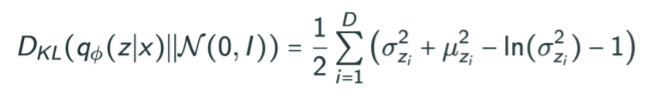
Variantional Auto-encoder의 가장 큰 단점은 Prior Fitting Term이 KL divergence을 활용한다는 것입니다.
즉, Gaussian이 아닐 때는 활용하기가 힘들다는 점이 있습니다.
2) Adversarial Auto-encoder
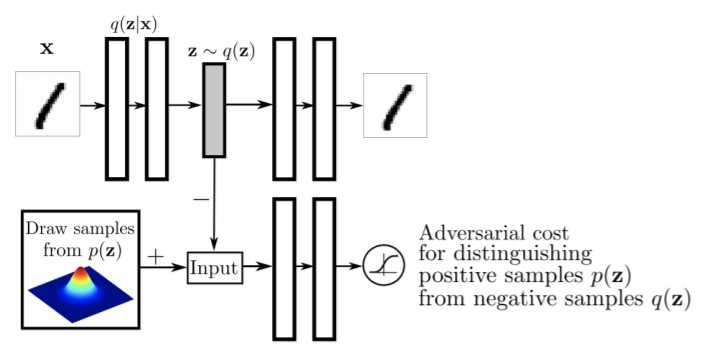
많은 경우에 Gaussian을 활용하지 않을 때 Adversarial Auto-encoder 사용합니다.
Adversarial Auto-encoder는 GAN을 사용해서 latent distribution 사이의 분포를 맞춰주는 방법을 사용합니다.
따라서 Adversarial Auto-encoder는 Variantional의 가장 큰 문제였던 Prior Fitting Term을 GAN으로 바꿔버린 것입니다.
그래서 latent distribution을 sampling만 가능하면 어떠한 분포(uniform 분포 등)가 있어도 해당 분포를 맞출 수 있습니다.
3️⃣ Generative Adversarial Network (GAN)
1) GAN

GAN은 위조지폐와 경찰 문제로 유명한 알고리즘입니다.
"위조지폐를 만드는 사람" (Generator)과 "경찰"(Discriminator)은 한쪽은 위조 지폐를 만들고 다른 한 쪽은 구별하는 법을 학습하면서 둘 다 함께 학습이 되는 구조를 가지게 됩니다.

이전 Variantional Auto-encoder는 $x$라는 이미지가 들어오면 encoder를 통해 $z$(latent vector)로 갔다가 decoder를 통해 다시 $x$를 출력하는 방법이었다면,
Generative Adversarial Networks는 $z$라는 latent distribution에서 출발해서 G(Generator)를 통해서 Fake가 생성되고, D(Discriminator)는 Real와 Fake를 구분하는 역할을 수행합니다. 이후, G(Generator)는 다시 D(Discriminator)에서 True가 나오도록 Generator를 업데이트하는 방법을 사용합니다.
즉, G(Generator)와 D(Discriminator)가 싸우는 게임이며, 이 게임을 통해서 둘 모두 학습하는 모델입니다.
G(Generator)와 D(Discriminator)는 아래 수식으로 표현됩니다.
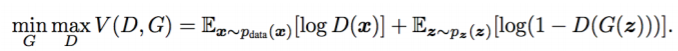
이때, Optimal discriminator $D^{*}_{G}(x)$은 아래와 같습니다.
Generator가 fix 되어있을 때 discriminator를 최적으로 만들어주는 것이 $D^{*}$입니다.
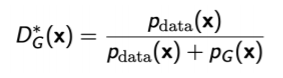
따라서 Optimal discriminator $D^{*}$를 다시 generator에 넣으면 아래와 같은 수식이 도출됩니다.

이 수식을 사용해서 generator를 갱신하고 다시 위의 과정을 반복해서 generator와 discriminator을 학습시킵니다.
2) DCGAN
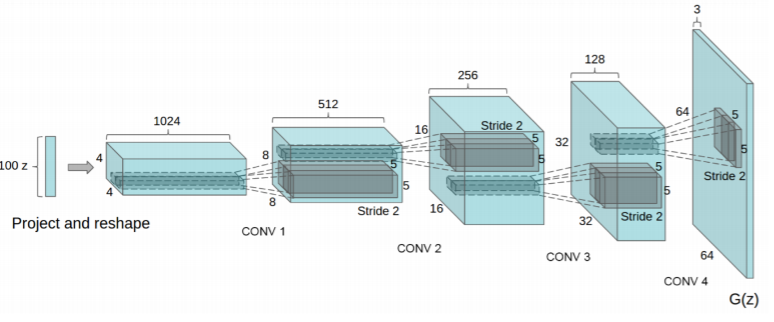
일반 GAN은 dense 형태로 만들었고, image layer로 만든 것이 DCGAN입니다.
3) Info-GAN

일반 GAN처럼 단순히 z 값을 통해서 이미지를 만들어내는 것이 아닌 c (class)를 랜덤하게 집어넣는 GAN입니다.
따라서 GAN이 특정 모드(one-hot vector, conditional vector)에 대해서 집중할 수 있게 만들어 줍니다.
4) Text2Image

어떤 문장을 image로 만들어주는 Generator입니다.
5) CycleGAN

GAN구조를 활용하면서 두 개의 image 사이의 도메인을 바꿀 수 있습니다.
예를 들어, 가운데 사진의 여러 마리의 horse(말)을 zebra(얼룩말)로 변환이 가능합니다.
아래 사진은 Cycle-consistency loss의 동작 방법입니다.
Cycle-consistency loss의 가장 큰 장점은 도메인을 찾아서 바꿔주는 역할입니다.
Cycle-consistency loss에는 GAN 구조가 2개가 들어갑니다.

4️⃣ Reference
생성모델(Generative model)이란 무엇일까?
내일이 기말고사라서 간단하게 강의 정리도 해야해서, 오늘은 비지도학습(Unsupervised learning) 중에서 클러스터링(Clustering)과 함께 가장 대표적인 예시 중 하나인 생성모델(Generative model)에 관련해
minsuksung-ai.tistory.com
'부스트캠프 AI 테크 U stage > 이론' 카테고리의 다른 글
| [17] RNN, LSTM, GRU 정리 (2) (0) | 2021.02.16 |
|---|---|
| [16] NLP 종류 / Bag-of-Words / Word Embedding (0) | 2021.02.15 |
| [14-1] Transformer 이해하기 (1) (0) | 2021.02.04 |
| [14] RNN, LSTM, GRU 정리 (1) (0) | 2021.02.04 |
| [13] CNN(Convolutional Neural Network) (0) | 2021.02.03 |




