| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Numpy
- boolean & fancy index
- unstack
- 최대가능도 추정법
- 카테고리분포 MLE
- Python 유래
- linalg
- 표집분포
- 딥러닝
- VSCode
- Python 특징
- Array operations
- seaborn
- type hints
- dtype
- 부스트캠프 AI테크
- 정규분포 MLE
- pivot table
- Operation function
- namedtuple
- BOXPLOT
- Python
- 가능도
- ndarray
- scatter
- Comparisons
- groupby
- subplot
- Numpy data I/O
- python 문법
- Today
- Total
또르르's 개발 Story
[14] RNN, LSTM, GRU 정리 (1) 본문
RNN은 Recurrent Neural Network의 약자로서, MLP(Multi Layer Perceptron)에 기반을 두고 있습니다.
하지만 RNN의 기본 모형은 많은 문제로 인해 LSTM, GRU 모델을 많이 사용합니다.
이번 시간에는 RNN, LSTM, GRU 모형에 대해 정리해보았습니다.
1️⃣ Sequence Data
RNN을 이해하기 위해서는 Sequence data에 대해서 이해해야 합니다.
sequence data는 순서에 따라 나열된 데이터를 뜻합니다.
소리, 문자열, 주가 등 모두 sequence data에 속하며, 특히 시계열(time-series) 데이터는 시간 순서에 따라 나열된 데이터로 sequence data에 속합니다. 시계열 데이터에는 소리, 주가 등이 포함됩니다.
Sequence data의 특징은 발생 순서가 중요하다는 것입니다.
예를 들어,
- 개가 사람을 물었다.
- 사람이 개를 물었다.
이렇게 순서를 바꿨을 때 문장의 의미가 완전히 달라지게 됩니다.
따라서 sequence data는 데이터 확률분포가 바뀌거나, 과거 정보로 미래를 예측할 때 과거의 정보에 손실이 발생해서 과거 데이터 일부분만 사용할 수 있는 경우, 데이터의 확률분포도 바뀌게 됩니다.
Sequence data는 조건부 확률(베이즈 법칙)을 이용합니다.
이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부 확률을 이용합니다.

Sequence data $P(X_{1}, ..., X_{t})$는 초기시점 $X_{1}$서부터 바로 직전의 정보인 $X_{t-1}$까지의 정보를 사용해서
현재 시점인 $X_{t}$를 모델링하는 확률분포를 반복적으로 곱하는 방법을 사용합니다.
따라서 아래와 같이 표현이 가능합니다.

그렇지만 sequence data는 "과거의 어떤 시점에서의 정보"는 필요하지 않을 때도 있기 때문에 필요성에 따라서
"과거의 정보를 어떻게 활용할 건지"에 대한 모델링이 중요합니다.
또한, sequence data에서 고정된 길이($\tau$)를 사용해서 모델링이 가능합니다.
이때, 고정된 길이 $\tau$만큼의 시퀀스만 사용하는 경우 AR($\tau$) (Autoregressive Model; 자기회귀모델)이라고 부릅니다.

또 다른 방법은 잠재변수 $H_{t}$를 사용해서 모델링하는 방법입니다.
이 방법은 현재 $t$를 제외한 나머지 정보들을 $H_{t}$라는 잠재변수로 summerize(요약)하는 방법입니다.(잠재 AR 모델)
이러한 모델을 Latent autoegressive model이라고 합니다.

잠재변수 $H_{t}$를 사용하면 $P(X_{t}|X_{t-1}*H_{t})$와 같이 고정된 길이로 모델링이 가능합니다.
잠재변수 $H_{t}$의 장점은
- 과거의 모든 데이터를 활용을 해서 예측을 할 수 있고
- 가변적인 데이터를 고정적인 데이터로 변경 가능합니다.

잠재변수 $H_{t}$를 신경망을 통해 반복해서 사용하여 sequence data의 패턴을 학습하는 모델이 바로 RNN입니다.

2️⃣ RNN (Recurrent Neural Network)
가장 기본적인 RNN 모형은 MLP와 유사합니다.
여기서 $W^{(1)}$는 첫 번째 가중치 행렬, $W^{(2)}$는 두 번째 가중치 행렬을 의미합니다.

1) RNN
RNN은 이전 순서의 잠재변수 $H_{t-1}$와 현재의 입력 $X_{t}$을 사용하여 $H_{t}$을 모델링합니다.
여기서 $W_{H}$는 이전 잠재 변수 $H_{t-1}$로부터 전달받게 되는 $W_{H}$입니다.

$W^{(1)}_{X}$는 현재 입력 데이터로부터 가중치를 뜻하고, $W_{H}$는 이전 시점에 잠재변수로부터 정보를 받아서 현재 시점의 잠재변수로 인코딩해주는 가중치를 뜻합니다.
위의 식에서 주목해야 할 점은 $W^{(2)}, W^{(1)}_{X}, W^{(1)}_{H}$은 t에 따라서 변하지 않는 가중치 행렬입니다. $t$에 따라서 변하는 것은 $X_{t}$와 $H_{t-1}$뿐입니다.
2) Short-term dependencies
Short-term dependencies는 어떤 시점에서 가까이 있는 과거는 기억할 수 있지만 멀리 있는 과거는 거의 기억을 못 하는 현상을 뜻합니다.
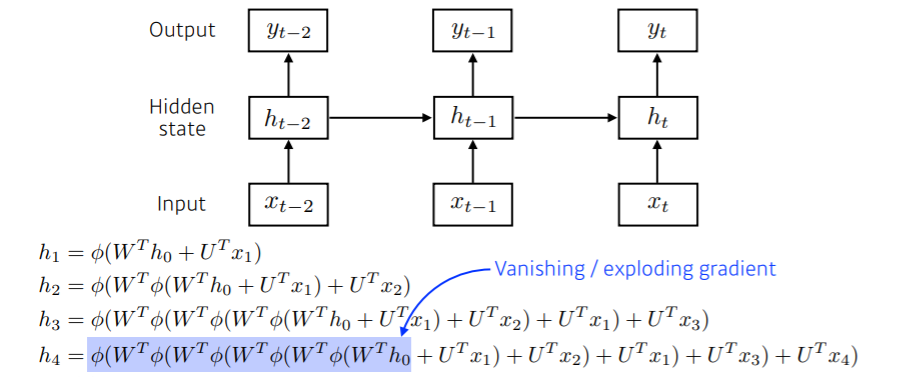
RNN은 계속 중첩되는 구조를 가지고 있기 때문에 $h_{4}$에서 $h_{0}$으로 갈려면 vanishing gradient를 경험합니다.
ReLU (위 식에서 $\phi$)를 쓰게 되면 가중치를 곱하고 activation을 통과하는 과정이 계속 반복되기 때문에 네트워크가 폭발해서 학습이 안 되는 현상이 발생합니다.
3) BPTT (Backpropagation Through Time)
RNN의 역전파에서는 입력으로 2개가 들어오게 됩니다.
다음 시점 $(t+1)$의 잠재변수에서 들어오는 그레디언트 벡터와 출력 $O(t)$에서 들어오는 그레디언트 벡터가 입력으로 들어옵니다.
RNN의 역전파는 Backpropagation Through Time (BPTT)라고 불립니다.

BPTT는 RNN의 가중치 행렬의 미분을 계산해보면 아래와 같이 미분의 곱으로 이루어진 항이 계산됩니다.
이때, $y$는 정답 레이블, $O$는 출력 값, $\ell$은 loss를 뜻합니다.

위 식의 마지막 라인에서 이 부분을 주의해야 합니다.
$$\left(\prod_{j=i+1}^{t} \partial_{h_{j-1}} f(x_{j},h_{j-1},w_{h})\right)$$
BPTT에서 위 항은 시퀀스 길이가 늘어나면 늘어날수록 1보다 크면 무한정 늘어나기 쉽고, 1보다 작으면 한없이 작아질 수가 있습니다. 그레디언트 계산을 계속 곱해주는 연산이기 때문이죠.
따라서 gradient 계산이 사라지는(영향을 거의 못 미치는) Vanishing gradient를 주의해야 합니다.
따라서 sequence 길이가 길어지는 경우, BPTT를 통한 역전파 알고리즘의 계산이 불안정해지기 때문에 길이를 끊는 것이 필요합니다. 이 과정을 truncated BPTT라 부르는데 미래 시점에서 몇 개의 시점만 가지고 와서 그레디언트 벡터를 계산하는 과정을 뜻합니다.
이러한 문제들 때문에 Vanilla RNN은 길이가 긴 sequence를 처리하는 게 힘듭니다.
이를 해결하기 위해 등장한 RNN 네트워크가 바로 LSTM과 GRU입니다.
3️⃣ LSTM (Long Short Term Memory)
LSTM은 Vanilla RNN에서 sequence 길이가 길어지면 학습이 안 되는 문제를 해결하기 위해 만들어진 구조입니다.
LSTM은 아래와 같은 구조를 가집니다.

LSTM 구조를 더 자세히 살펴보면 아래와 같습니다.

previous cell state는 네트워크 내부에서만 흘러가고, $1$부터 $t-1$의 정보를 다 취합해서 요약해준 정보를 뜻합니다.
previous hidden state는 나가는 output정보입니다.
따라서 실제로 나가는 값(출력되는 값)은 output(hidden state)밖에 없습니다.
1) Forget Gate : 어떤 정보를 버릴지

여기서 "[ ]"가 concat 하는 것을 뜻합니다.
현재 입력 $x_{t}$와 이전의 output $h_{t-1}$이 들어가서 $f_{t}$라는 숫자(값)를 얻어내게 됩니다.
위 식은 sigmoid $\sigma$를 통과하기 때문에 $f_{t}$는 항상 0~1사이의 값입니다.
$f_{t}$는 cell state에서 나오는 정보 중에 어떤 값을 버리고 살릴지를 결정하는 역할을 합니다.
즉, cell state를 버리고 살릴지 결정하는 것은 현재 입력 $x_{t}$와 이전의 output $h_{t-1}$을 통해 결정이 됩니다.
2) Input Gate : 어떤 정보를 cell state에 추가할지

$i_t$는 어떤 정보를 추가할지 말지를 현재 입력 $x_{t}$와 이전의 output $h_{t-1}$을 사용해서 결정합니다.
$\tilde{c} _{t}$는 추가할 정보의 내용을 뜻하며, 현재 입력 $h_{t-1}, x_{t}$을 "따로 학습되는 neural network" (가중치가 $W_{C}$)에 집어넣고 $\tanh$ (정규화)을 취해준 값입니다.
3) Update Gate : cell state 업데이트
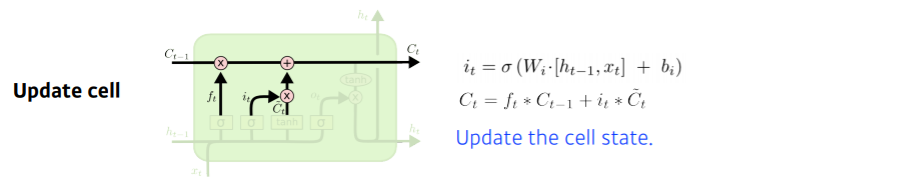
Update Gate는 previous cell state와 $C_{t}$를 잘 조합해서 새로운 cell state로 update 하는 과정입니다.
$$C_{t} (새로운 cell state) = f_{t} * C_{t-1}(버릴 것은 버리고) + i_{t} * \tilde{C}_{t}(새롭게추가)$$
4) Output Gate : 어떤 값을 내보낼지

$o_{t}$는 어떤 값을 밖으로 내보낼지를 결정합니다.
$o_{t}$를 사용해서 $h_{t}$ (output)을 내보내고, 다음 previous hidden state로 보냅니다.
4️⃣ GRU (Gated Recurrent Unit)
GRU는 LSTM에서 parameter를 줄인 모델입니다.
LSTM보다 GRU 성능이 더 좋다는 실험적인 결과가 있는데요. 그 이유는 parameter가 적기 때문에 generlization performance가 올라가기 때문입니다. (하지만 요즘에는 다 Transformer를 사용하는 추세..)
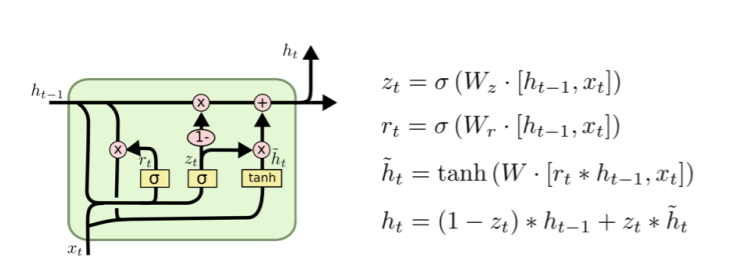
GRU는 reset gate와 update gate, 2개의 gate를 사용합니다.
GRU의 특징은 cell state가 없고 hidden state가 곧 output이며, 다음 순서의 previous hidden state를 나타냅니다.
또한, output gate가 없습니다.
5️⃣ 추가 내용
추가 내용은 RNN, LSTM, GRU 정리(2)에서 정리하겠습니다.
[17] Vanilla RNN / LSTM / GRU 정리
1️⃣ Vanilla RNN 예측값을 나타내는 y_t는 매 타임스텝에 계산해야할 때도 있고 마지막 타임스텝에 계산해야할 때도 있습니다. ex) 문장에서 각 품사를 예측 -> 매 타음스텝마다 계산, 문장이 긍정
dororo21.tistory.com
'부스트캠프 AI 테크 U stage > 이론' 카테고리의 다른 글
| [15] Generative Models (0) | 2021.02.05 |
|---|---|
| [14-1] Transformer 이해하기 (1) (0) | 2021.02.04 |
| [13] CNN(Convolutional Neural Network) (0) | 2021.02.03 |
| [12-1] Convolution 연산 이해하기 (0) | 2021.02.03 |
| [12] 최적화 (Optimization) 종류와 용어들 (0) | 2021.02.02 |




