[25] 그래프 신경망

1️⃣ 그래프 신경망

 

그래프 신경망은 그래프와 정점의 속성 정보를 입력으로 받습니다.

 

그래프의 인접 행렬을 A라고 합시다. 인접 행렬 A 은 |𝑉| × |𝑉|의 이진 행렬입니다

각 정점 𝑢의 속성(Attribute) 벡터를 $𝑋_{𝑢}$라고 합시다. 정점 속성 벡터 $𝑋_{𝑢}$는 𝑚차원 벡터이고, 𝑚은 속성의 수를 의미합니다.

 

그래프 신경망은 이웃 정점들의 정보를 집계하는 과정을 반복하여 임베딩을 얻습니다.

아래 그림처럼 대상 정점의 임베딩을 얻기 위해 이웃들 그리고 이웃의 이웃들의 정보를 집계합니다.

 

http://snap.stanford.edu/proj/embeddings-www/

 

A가 우리가 얻고자 하는 대상 정점일때,

A(대상 정점) -> 한 단계 인접한 그래프 정보 집계 -> 2단계 인접한 그래프 정보 집계를 차례차례 수행합니다.

(여기서 2단계를 집계할 때 A가 다시 등장하는 것을 알 수 있음)

 

http://snap.stanford.edu/proj/embeddings-www/

 

각 집계 단계를 층(Layer)이라고 부르고, 각 층마다 임베딩을 얻습니다.

각 층에서는 이웃들의 이전 층 임베딩을 집계하여 새로운 임베딩을 얻습니다.

0번 층, 즉 입력 층의 임베딩으로는 정점의 속성 벡터($X_{A}, X_{C}, X_{F} ...$)를 사용합니다.

 

http://snap.stanford.edu/proj/embeddings-www/

 

따라서 대상 정점마다 집계되는 정보가 상이합니다.

대상 정점 별 집계되는 구조를 계산 그래프(Computation Graph)라고 부릅니다.

 

https://www.edwith.org/bcaitech1

 

대상 정점마다 집계되는 정보가 상이하기 때문에 parameter들이 너무 많아질 우려가 있어 서로 다른 대상 정점 간에도 층 별 집계 함수는 공유합니다. (다만, 다른 층에서 사용하는 집계함수는 공유하지 않음)

 

https://www.edwith.org/bcaitech1

 

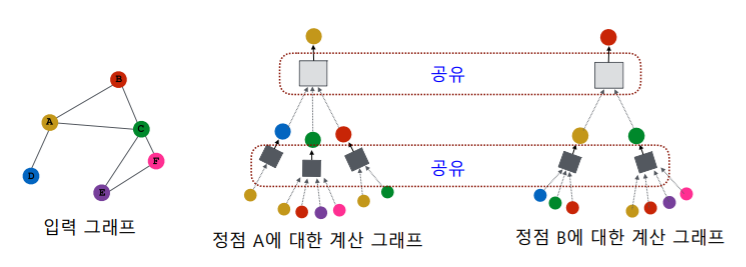
서로 다른 구조의 계산 그래프를 처리하기 위해서는 어떤 형태의 집계 함수가 필요할까요?

왜냐하면 위의 그림에서 입력의 크기가 가변적이어도 처리할 수 있는 형태(공유하기 때문에)여야 하기 때문입니다.

따라서 그래프 신경망에서의 집계 함수는 (1) 이웃들 정보의 평균을 계산하고 (2) 신경망에 적용하는 단계를 거칩니다.

 

https://www.edwith.org/bcaitech1

 

"평균"을 내면 입력에 2개던 4개던 모두 하나의 값으로 축소가 됩니다. 따라서 어떠한 입력의 크기도 받을 수 있습니다.

 

1) 집계함수

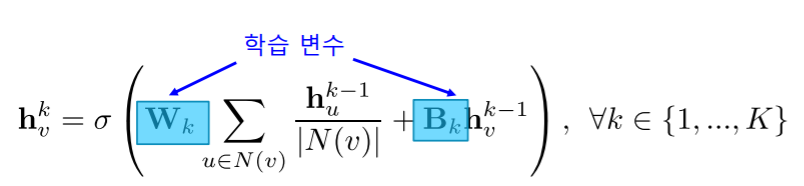
집계함수를 수식으로 표현하면 다음과 같습니다.

 

• $h^{k-1}_{u}$ : 이웃들에 대한 $k-1$ 번째 층에서의 임베딩
• $h^{k-1}_{v}$ : 자기 자신에 대한 $k-1$ 번째 층에서의 임베딩
• $W_{k}$ : 이웃에 대한 신경망 가중치
• $B_{k}$ : 자기 자신에 대한 신경망 가중치

https://www.edwith.org/bcaitech1

 

0번째 층에서의 임베딩은 입력 속성 정보를 넣어줍니다.

 

$$h^{0}_{v} = X_{v}$$

 

마지막 층에서의 임베딩은 출력 임베딩입니다.

 

$$z_{v} = h^{K}_{v}$$

 

그래프 신경망의 학습 변수(Trainable Parameter)는 층 별 신경망의 가중치입니다.

 

https://www.edwith.org/bcaitech1

 

2) 손실함수

그래프 신경망에서의 손실함수는정점 간 거리를 “보존”하는 것을 목표입니다.

만약, 인접성을 기반으로 유사도를 정의한다면, 손실 함수는 다음과 같습니다.

 

https://www.edwith.org/bcaitech1

 

후속 과제(Downstream Task)의 손실함수를 이용한 End-to-End 학습도 가능합니다.

(즉, 처음부터 끝까지 전체 프로세스에 해당 손실함수를 사용하는 것)

 

정점 분류가 최종 목표인 경우,

 

(1) 그래프 신경망을 이용하여 정점의 임베딩을 얻고

(2) 이를 분류기(Classifier)의 입력으로 사용하여

(3) 각 정점의 유형을 분류

 

하는 과정을 거치게 됩니다.

 

즉, 최종 목표가 정점 분류일 때, 임베딩을 얻지만 그 임베딩을 classifier에 통과시켜서 분류하는 것이 목표입니다. 이런 경우에는 vector의 임베딩이 그래프에서의 유사도를 보존하는지 보존하지 않는지는 직접적인 관심사는 아니게 됩니다.

 

우리의 관심은 임베딩 vector를 사용해서 분류기를 통과시켰을 때 정확도가 얼마나 높은지, 그 정확도를 높이는 것이 우리의 직접적인 목표입니다. 이러한 직접적인 목표를 달성하기 위해서는 직접적인 목표와 더욱 관련된 손실함수를 사용해야 합니다.

 

그래서 분류기의 정확도를 높이는 것이 목표라면 Cross Entropy와 같은 손실함수를 주로 사용합니다. 교차 엔트로피(Cross Entropy)를, 전체 프로세스의 손실함수로 사용하여 End-to-End 학습을 할 수 있습니다. 이러한 손실함수를 사용한다는 것은 분류기의 학습 변수를 통해 분류의 정확도가 제일 높아지게끔 그래프 신경망의 학습 변수들을 학습하라는 의미가 담겨져 있습니다.

 

https://www.edwith.org/bcaitech1

 

3) 오차역전파(Backpropagation)와 예측(Predict)

Loss까지 정했다면 학습에 사용할 대상 정점을 결정하여 학습 데이터를 구성합니다.

선택한 대상 정점들에 대한 계산 그래프를 구성합니다.

 

http://snap.stanford.edu/proj/embeddings-www/

 

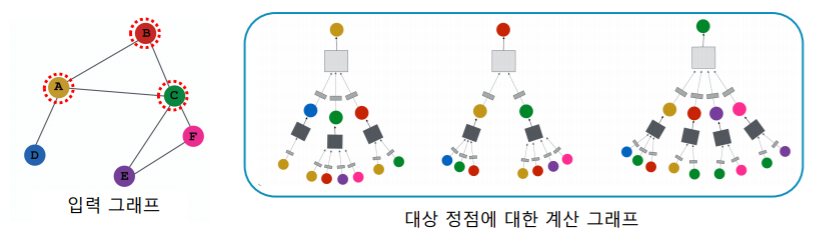
이후, 오차역전파(Backpropagation)을 통해 손실함수를 최소화합니다.

즉, 오차역전파를 통해 신경망의 학습 변수들을 학습합니다.

 

http://snap.stanford.edu/proj/embeddings-www/

 

학습된 신경망을 적용하여, 학습에 사용되지 않은 정점의 임베딩(Predict)을 얻을 수 있습니다.

 

https://www.edwith.org/bcaitech1

 

 

2️⃣ 그래프 합성곱 신경망 (GCN)

 

그래프 합성곱 신경망(Graph Convolutional Network, GCN)은 다른 집계함수를 사용합니다.

 

https://www.edwith.org/bcaitech1

 

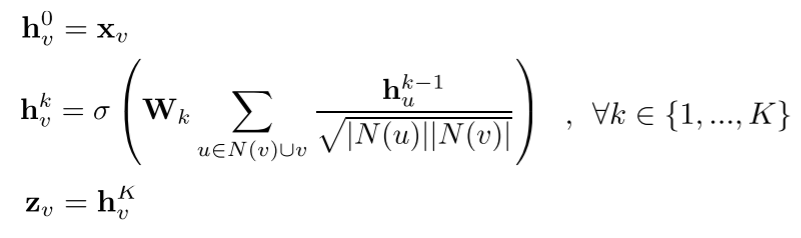
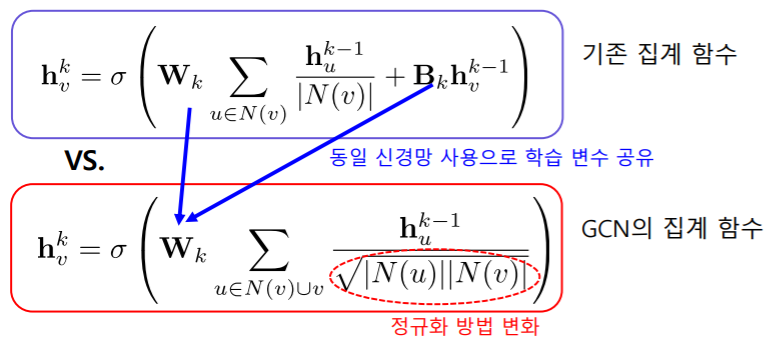
즉, 기존 집계함수와 비교하면 다음과 같은 다른 점이 있습니다.

 

• 기존에는 $W_k, B_k$를 사용해서 따로 parameter를 갱신했지만, GCN에서는 $W_k$로 통일
• $\sqrt(|N(u)||N(v)|)$는 $u$와 $v$ 연결성의 기하평균

https://www.edwith.org/bcaitech1

 

3️⃣ GraphSAGE

 

GraphSAGE는 AGG 함수를 사용해서 집계함수를 정의합니다.

이웃들의 임베딩을 AGG 함수를 이용해 합친 후, 자신의 임베딩과 연결(Concatenation)하는 점이 독특합니다.

 

https://www.edwith.org/bcaitech1

 

여기서 나오는 AGG 함수는 평균, 풀링, LSTM 등이 사용될 수 있습니다.

 

https://www.edwith.org/bcaitech1

 

4️⃣ 합성곱 신경망(CNN) vs 그래프 신경망(GCN)

1) 유사성

합성곱 신경망과 그래프 신경망은 모두 이웃의 정보를 집계하는 과정을 반복합니다.

 

2) 차이점

합성곱 신경망은 이웃 픽셀의 의미 있는 정보를 집계하는 과정을 반복합니다.

아래 그림에서 가운데 주황색 값을 얻기 위하여, 이웃 8개의 픽셀의 정보를 집계하는 방법을 사용합니다.

합성곱 신경망에서 주변에 있는 이웃 픽셀은 대상 정점에 의미가 있는 픽셀일 확률이 높으며, 합성곱을 통해 의미를 추출해냅니다.

 

http://snap.stanford.edu/proj/embeddings-www/

 

그래프 신경망의 인접행렬에서는 $i-1, i+1$ 행은 우연히 거기에 있을 뿐, 대상 정점 $i$와는 아무런 연관성이 없습니다.

그래서 $i$의 정보를 구하기 위해 아무 연관이 없는 $i-1, i+1$의 정보를 사용하는 것은 비효율적입니다.

 

https://www.edwith.org/bcaitech1

 

또한, 합성곱 신경망에서는 이웃의 수가 균일하지만, 그래프 신경망에서는 아닙니다.

그래프 신경망에서는 정점 별로 집계하는 이웃의 수가 다릅니다.

 

http://snap.stanford.edu/proj/embeddings-www/

 

5️⃣ 그래프 어텐션 신경망(GAT)

 

기본 그래프 신경망에서는 이웃들의 정보를 동일한 가중치로 평균을 냅니다.

그래프 합성곱 신경망에서 역시 단순히 연결성을 고려한 가중치로 평균을 냅니다.

 

그래프 어텐션 신경망(Graph Attention Network, GAT)에서는 가중치 자체도 학습합니다.

실제 그래프에서는 이웃 별로 미치는 영향이 다를 수 있기 때문입니다. 가중치를 학습하기 위해서 셀프-어텐션(Self-Attention)이 사용됩니다.

 

https://www.edwith.org/bcaitech1

 

1) Self-Attention

각 층에서 정점 𝑖로부터 이웃 𝑗로의 가중치 $𝜶_{𝒊𝒋}$는 세 단계를 통해 계산합니다.

 

https://www.edwith.org/bcaitech1

 

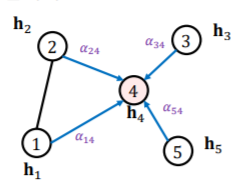
1) 해당 층의 정점 𝑖의 임베딩 $𝐡_{𝑖}$에 신경망 𝑾를 곱해 새로운 임베딩 $\tilde{h}_{i}$을 얻습니다.

 

2) 정점 𝑖와 정점 𝑗의 새로운 임베딩을 연결(concat) 한 후, 어텐션 계수 𝒂를 내적 합니다. 어텐션 계수 𝒂는 모든 정점이 공유하는 학습 변수입니다.

(여기서 내적이 아닌 Concat을 하는 이유는 $\tilde {h}_{i}, \tilde {h}_{j}$가 각각의 가중치 $W_{i}, W_{j}$를 가지므로, 내적을 하게 되면 $\tilde {h}_{i} \cdot \tilde {h}_{j} = h_{i}W_{i}\cdot h_{j}W_{j}$로 $W_i, W_j$의 의미가 $W$로 병합되기 때문에)

 

 

3) 2)의 결과에 소프트맥스(Softmax)를 적용합니다.

 

 

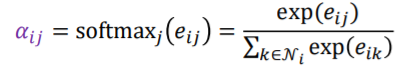
2) Multi-head Attention

여러 개의 어텐션을 동시에 학습한 뒤, 결과를 연결하여 사용합니다.

 

• $k$ : Multi-head로 나누는 개수
  
  
• $\alpha_{ij}^{k}$ : k개로 나눈 정점 $i$에서 정점 $j$까지의 가중치

 

$k$는 다음과 같이 나눠져서 (여기서는 3개) 각각의 가중치 $W_{k}$와 곱해집니다.

 

 

따라서 3개의 Attention을 사용한 GAT은 다음과 같이 표현됩니다.

즉, $h_{1}^{'}$을 구하기 위해 대상 정점 $h_{1}$과 이웃 $h_{2}, h_{3}, h_{4}, h_{5}, h_{6}$ 사이의 관계를 계산한 $\alpha_{11}$과 $\alpha_{12}, \alpha_{13}, \alpha_{14}, \alpha_{15}, \alpha_{16}$ 의 값들을 곱한 후 더해서 $h_{1}^{'}$를 구합니다.

이때, 보라색, 파란색, 초록색 선은 각각의 Multi-head들을 나타내고, $W_{보락색}$, $W_{파란색}$, $W_{초록색}$ 가중치를 곱해줍니다.

 

https://arxiv.org/pdf/1710.10903.pdf

 

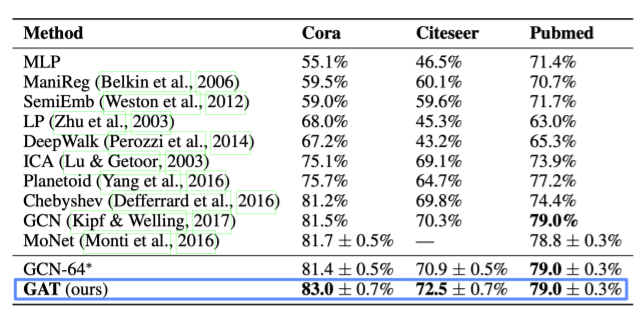
어텐션의 결과 정점 분류의 정확도(Accuracy)가 향상되는 것을 확인할 수 있었습니다.

 

https://arxiv.org/pdf/1710.10903.pdf

 

 

6️⃣ 그래프 표현 학습과 그래프 풀링

1) 그래프 표현 학습

그래프 표현 학습, 혹은 그래프 임베딩이란 그래프 전체를 벡터의 형태로 표현하는 것입니다.

그래프 임베딩은 벡터의 형태로 표현된 그래프 자체를 의미하기도 합니다.

 

그래프 임베딩은 그래프 분류 등에 활용됩니다.

그래프 형태로 표현된 화합물의 분자 구조로부터 특성을 예측하는 것이 한 가지 예시입니다.

 

2) 그래프 풀링 (Graph Pooling)

그래프 풀링(Graph Pooling)이란 정점 임베딩들로부터 그래프 임베딩을 얻는 과정입니다.

 

평균 등 단순한 방법보다 그래프의 구조를 고려한 방법을 사용할 경우 그래프 분류 등의 후속 과제에서 더 높은 성능을 얻는 것으로 알려져 있습니다.

 

아래 그림의 미분가능한 풀링(Differentiable Pooling, DiffPool)은 군집 구조를 활용 임베딩을 계층적으로 집계합니다. 즉, 군집 구조를 이용해서 군집별로 임베딩 합산합니다.

 

https://arxiv.org/pdf/1806.08804.pdf

 

미분 가능한 풀링에는 그래프 신경망이 여러 곳에서 사용됩니다.

 

• 개별 정점의 임베딩을 얻는 데 사용
• 정점들을 군집 구조로 묶는데도 사용
• 군집 내에서 합산할 때에도 사용

 

7️⃣ 지나친 획일화 문제

 

지나친 획일화(Over-smoothing) 문제란 그래프 신경망의 층의 수가 증가하면서 정점의 임베딩이 서로 유사해지는 현상을 의미합니다.

 

즉, 층을 5개 쌓게 되면 5만큼 떨어진 정점들의 정보를 집계하게 되는데 많은 정점들의 사이가 가깝다 보니까(작은 세상 효과) 거리 5 정도면 수많은 정점들의 정보를 가지고 합산하게 됩니다. 따라서 그래프의 지역 부분이 아닌 그래프 전반을 집계하는 현상이 나옵니다. 그렇게 되면 정점들이 비슷비슷한 임베딩을 갖게 되고, 분류의 성능이 떨어지게 됩니다.

 

https://ojs.aaai.org/index.php/AAAI/article/view/11604

 

지나친 획일화의 결과로 그래프 신경망의 층의 수를 늘렸을 때, 후속 과제에서의 정확도가 감소하는 현상이 발견되었습니다. 아래 그림에서 보듯이 그래프 신경망의 층이 2개 혹은 3개 일 때 정확도가 가장 높습니다. Residual 방법을 사용하는 것도 약간은 나아지지만 효과가 제한적입니다.

 

https://www.edwith.org/bcaitech1

 

획일화 문제에 대한 대응으로는 2가지가 있습니다.

 

• JK 네트워크(Jumping Knowledge Network)

모든 층의 임베딩을 최종 집계함수에 넣어줘서 최종 임베딩을 얻는 방식을 사용합니다.

 

https://arxiv.org/pdf/1810.05997.pdf

 

• APPNP

APPNP는 0번째 층을 제외하고는 신경망 없이 집계 함수를 단순화하였습니다. 가중치 $W$ 행렬을 0번째 layer에만 넣고 1,2,3 번째 lalyer에서는 $W$를 없이 해서 집계함수 자체를 단순화시켰습니다.

 

https://arxiv.org/pdf/1806.03536.pdf

 

즉, APPNP는 층의 수를 쌓는다 하더라도 가중치 $W$는 늘어나지 않으며, 다른 그래프 신경망과 비교했을 때 성능을 유지하거나 조금 더 좋아지는 것을 알 수 있습니다.

 

https://www.edwith.org/bcaitech1

 

 

8️⃣ 데이터 증강 (Data Augmentation)

 

데이터 증강(Data Augmentation)은 다양한 기계학습 문제에서 효과적입니다.

 

그래프에도 누락되거나 부정확한 간선이 있을 수 있고, 데이터 증강을 통해 보완할 수 있습니다. 임의 보행을 통해 정점 간 유사도를 계산하고, 유사도가 높은 정점 간의 간선을 추가하는 방법이 제안되었습니다.

 

Input data에서 정점의 유사도가 특별히 높은 것들만 필터링한 후, 필터링한 값과 input data의 간선들을 더해줘서 간선이 추가된 그래프를 얻고 그래프 신경망의 입력으로 넣어주는 방법입니다.

 

 

https://arxiv.org/abs/1911.05485

 

그래프 데이터 증강의 결과 정점 분류의 정확도가 개선되는 것을 확인했습니다.

아래 그림의 HEAT과 PPR은 제안된 그래프 데이터 증강 기법을 의미합니다.

 

https://arxiv.org/abs/1911.05485

 

[실습 1]

이것을 구현

AGG는 평균으로 계산