[06-1] 벡터와 행렬 with Python Numpy

05-1에서는 머신러닝의 가장 기본이 되는 벡터와 행렬을 정리해보겠습니다.

작성하면서 Python의 numpy에서 어떤 함수로 사용되는지를 함께 정리하겠습니다. (강의 내용 정리...)

 

 

1️⃣ 벡터(Vector)

 

벡터(vector)는 숫자를 원소로 가지는 리스트(list) 또는 배열(array)라고 말할 수 있습니다.

https://www.edwith.org/bcaitech1

또한, vector는 세로형태의 열 벡터와 가로형태의 행 벡터로 나눌 수 있습니다.

https://www.edwith.org/bcaitech1

수학적인 벡터의 정의는 공간에서 한 점을 나타내며, 원점으로부터 상대적인 위치를 표현한 것을 말합니다.

아래 그림과 같이 X는 1차원, 2차원, 3차원에서 하나의 점이며, 원점으로부터 방향이 있습니다.

https://www.edwith.org/bcaitech1

 

1) 벡터의 덧셈

 

두 벡터의 덧셈은 다른 벡터로부터 상대적 위치 이동을 표현합니다.

즉, 아래의 그림처럼 X의 벡터의 원점을 y로 옮기는 것이 벡터의 덧셈입니다.

https://www.edwith.org/bcaitech1

 

2) 벡터의 뺄셈

 

두 벡터의 뺄셈은 벡터의 방향을 뒤집은 덧셈을 표현합니다.

https://www.edwith.org/bcaitech1

 

3) 노름(norm)

 

벡터의 노름(norm)은 원점에서부터의 거리를 말합니다.

 

노름은 2가지(L1-노름, L2-노름)가 있습니다.

 

- L1-노름 : 맨해튼 거리 공식

Python에서는 아래와 같이 표현할 수 있습니다.

def l1_norm(x):

    x_norm = np.abs(x)
    
    x_norm = np.sum(x_norm)
    
    return x_norm

 

- L2-노름 : 유클리드 거리 공식

Python에서는 아래와 같이 표현할 수 있습니다.

def l2_norm(x):

    x_norm = x*x
    
    x_norm = np.sum(x_norm)
    
    x_norm = np.sqrt(x_norm)
    
    return x_norm

또는, np.linalg.norm을 사용해서 계산이 가능합니다.

>>> np.linalg.norm(x)

 

두 개의 노름은 기하학적인 성질이 다르므로 머신러닝에서는 각 노름의 성질을 사용할 때가 있습니다.

 

 

4) (노름을 이용한) 두 벡터 사이의 거리

 

그렇다면 두 벡터의 거리를 계산해봅시다. 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용합니다.

즉, L1-노름 또는 L2-노름을 이용해서 벡터의 뺄셈을 해서 두 벡터 사이의 거리를 계산할 수 있습니다.

https://www.edwith.org/bcaitech1

 

5) (노름을 이용한) 두 벡터 사이의 각도

 

이번에는 두 벡터의 사이의 각도를 계산해봅시다. 두 벡터 사이의 각도를 계산할 때도 노름을 사용합니다.

하지만 주의해야 할 점은 L2-노름만 사용 가능하다는 것입니다.

 

각도를 계산하기 위해서는 $\Theta$ 값을 구해야 합니다. $\Theta$를 구하기 위해서는 제2 코사인 법칙을 사용합니다.

$cos\Theta$를 계산하기 위해서는 분모와 분자를 각각 계산해주어야 하는데 내적을 사용하면 쉽게 계산할 수 있습니다.

내적은 $<x,y>$로 표현합니다.

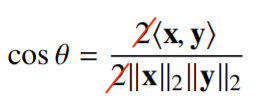
$cos\Theta$를 계산하게 되면 $\Theta$를 계산해야 합니다.

$\Theta$는 $cos\Theta$값에 $arccos$을 사용하면 $\Theta$값을 구할 수 있습니다.

>>> theta = np.arccos(X)

 

 

6) (노름을 이용한) 내적

 

내적을 구할 수 있다면 $cos\Theta$를 쉽게 계산할 수 있습니다.

그렇다면 내적은 무엇일까요?

 

내적은 벡터의 곱셈입니다. 벡터의 곱셈에는 여러 가지 종류가 있는데 그중 하나라고 생각하시면 됩니다.

백터의 곱셈을 해야 하는데 여러 방향으로 뻗어있는 벡터를 어떻게 모아서 곱셈을 시킬 것이냐.. 이 것이 문제입니다.

 

그래서 내적은 정사영이라는 개념을 사용합니다.

정사영은 그림자의 의미로 X의 벡터가 Y 벡터로 수직으로 내리꽂은 값입니다.

https://www.edwith.org/bcaitech1

이렇게 정사영을 사용하면 X 벡터와 Y 벡터가 한 직선에 있기 때문에 곱셈이 가능하며, Scalar값(정수)으로 표현이 가능합니다.

(정사영의 의미를 더 자세히 설명하자면 X 벡터가 Y벡터의 방향이 되었을 때 가지고 있는 힘의 크기라고 말할 수 있습니다.)

 

따라서 X의 정사영 Proj(X)는 $\left \| X \right \| cos \Theta$로 표현할 수 있으며,

내적 $<x,y>$는

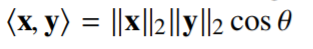
라고 표현할 수 있습니다.

 

Python numpy를 사용하면 아래 명령어로 한 번에 계산이 가능합니다.

np.inner(x, y)

 

 

2️⃣ 행렬(Matrix)

 

행렬(Matrix)은 벡터를 원소로 가지는 2차원 배열입니다. 

https://www.edwith.org/bcaitech1

행렬은 행(row)과 열(column)이라는 인덱스(index)를 가집니다.

아래 그림과 같이 i는 행(row)을 나타내며, j는 열(column)을 나타냅니다.

 

1) 행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱

 

행렬의 덧셈, 뺄셈은 행렬끼리 같은 모양을 가지면 계산할 수 있습니다.

https://www.edwith.org/bcaitech1

행렬의 성분곱도 행렬끼리 같은 모양을 가지면 계산이 가능합니다.

다만, 곱셈이 아니기 때문에 $\odot $으로 표현합니다.

https://www.edwith.org/bcaitech1

행렬의 스칼라곱은 모든 성분에 스칼라 값을 계산합니다.

https://www.edwith.org/bcaitech1

 

2) 행렬의 곱셈

 

행렬의 곱셈은 i 번째 행 벡터와 j 번째 열 벡터 사이의 내적을 성분으로 가지는 행렬입니다.

따라서 중요한 점은 X의 열의 개수와 Y의 행의 개수가 같아야 계산이 가능합니다.

https://www.edwith.org/bcaitech1

Python Numpy에서는 '@'을 사용하여 곱셈을 할 수 있습니다.

X = np.array([[1, -2, 3],
              [7, 5, 0],
              [-2, -1, 2]])
             
Y = np.array([[0, 1],
              [1, -1],
              [-2, 1]])
              
              
>>> X @ Y

array([[-8, 6],
       [ 5, 2],
       [-5, 1]])
             

 

3) 행렬의 내적 (np.inner)

 

Python numpy의 np.inner은 행렬에서 사용할 수 있지만 수학에서 말하는 내적 하고 다르므로 주의해야 합니다.

numpy의 np.inner은 i번째 행 벡터와 j번째 행벡터 사이의 내적을 말합니다. 

 

즉, 수학적으로 말하면 $tr(XY^T)$이라고 말할 수 있습니다.

https://www.edwith.org/bcaitech1

Python numpy를 사용하면 아래와 같습니다.

X = np.array([[1, -2, 3],
              [7, 5, 0],
              [-2, -1, 2]])
             
Y = np.array([[0, 1, -1],
              [1, -1, 0]])
              
              
>>> np.inner(X, Y)

array([[-5, 3],
       [ 5, 2],
       [-3,-1]])
             

 

4) 역행렬

 

어떤 행렬 $A$의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이라 부르고 $A^{-1}$라고 표현합니다.

역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있습니다.

Python에서는 np.linalg.inv를 사용하면 역행렬을 계산할 수 있습니다.

X = np.array([[1, -2, 3],
              [7, 5, 0],
              [-2, -1, 2]])
 

>>> np.linalg.inv(X)

array([[ 0.21276596,  0.0212766 , -0.31914894],
       [-0.29787234,  0.17021277,  0.44680851],
       [ 0.06382979,  0.10638298,  0.40425532]])

 

5) 유사 역행렬(pseudo-inverse)

 

역행렬 $A^{-1}$는 무조건 행과 열 숫자가 같은 경우입니다. 하지만 현실적으로 계산을 해보면 그렇지 않은 경우가 훨씬 많습니다. 이러한 경우는 유사 역행렬(pseudo-inverse)을 사용합니다.(또는 무어 펜로즈(Moore-Penrose) 역행렬이라고 합니다.)

 

유사 역행렬(pseudo-inverse)의 표기는 $A^{+}$로 합니다.

주의할 점은 A의 행(n)과 열(m)의 크기에 따라 계산이 달라집니다.

Python에서는 np.linalg.pinv를 사용하면 유사 역행렬을 계산할 수 있습니다.

X = np.array([[1, -2],
              [7, 5],
              [-2, -1]])
              

>>> np.linalg.pinv(X)

array([[ 0.25316456,  0.08860759, -0.06329114],
       [-0.36202532,  0.06329114,  0.04050633]])

 

유사 역행렬은 연립방정식, 선형 회귀분석 등 다양한 곳에 사용이 가능합니다.

 

- 연립방정식

https://www.edwith.org/bcaitech1

- 선형회귀분석

선형 회귀분석의 경우 점(빨간 점)의 경우 모두 선형에 일치하지 않으므로, 일치 값 $y$가 아닌 근삿값 $\hat{y}$을 사용합니다. 근삿값 $\hat{y}$를 사용해서 유사 역행렬로 $\beta$를 구할 수 있습니다.

https://www.edwith.org/bcaitech1