| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Python
- 최대가능도 추정법
- Python 유래
- Numpy data I/O
- VSCode
- Numpy
- 정규분포 MLE
- Array operations
- groupby
- Python 특징
- 카테고리분포 MLE
- BOXPLOT
- dtype
- unstack
- scatter
- Operation function
- namedtuple
- subplot
- 가능도
- linalg
- seaborn
- ndarray
- pivot table
- 딥러닝
- boolean & fancy index
- Comparisons
- 부스트캠프 AI테크
- python 문법
- type hints
- 표집분포
- Today
- Total
또르르's 개발 Story
[07] 경사하강법 본문
경사하강법은 1차원, 2차원.. 다차원의 그래프에서 최솟값(극소값)을 찾아가는 방법을 말합니다.
아래 그림과 같이 다차원의 그래프에서 가장 오목하게 들어간 부분(최솟값)을 찾아가는 과정이라는 것이죠.

경사하강법을 정리하게 전에 미분부터 알아야 합니다.
1️⃣ 미분(Differentiation)
미분(differentiation)은 변수의 움직임(그래프)에 따른 함수값의 변화(기울기)를 측정하기 위한 도구로 수학에서 정의합니다. 미분은 $f^{'}$으로 표시하며 아래 식으로 표현됩니다.
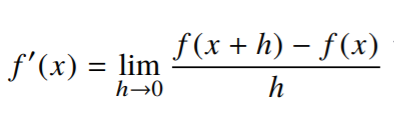
다항식의 경우, 아래와 같이 표현할 수 있습니다.
$$ f(x) = x^2 + 2x +3$$
미분 공식을 사용하게 되면 아래 다항식으로 변경됩니다.
$$f^{'}(x) = 2x + 2$$
Python에서는 sympy 모듈을 사용하면 쉽게 미분이 가능합니다. (conda install sympy 설치 요망)
import sympy as sym
from sympy.abc import x
>>> sym.diff(sym.poly(x**2 + 2*x + 3), x)
Poly(2𝑥+2,𝑥,𝑑𝑜𝑚𝑎𝑖𝑛=ℤ)
그렇다면 경사하강법에는 미분을 어떻게 사용할까요?
2️⃣ 경사상승 / 경사하강
미분은 접선의 기울기를 나타냅니다.
접선의 기울기를 사용하면 함수 그래프의 최소값과 최대값을 찾을 수 있습니다.
접선의 기울기는 어떤 한 점 $x$에서 기울기를 나타내기 때문에
- 함수가 상승하면 $f^{'}(x) > 0$
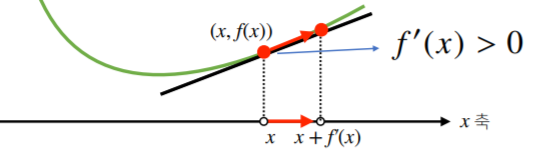
- 함수가 하강하면 $f^{'}(x) < 0$

을 나타내게 됩니다.
이 점을 이용해서 $x$에서 $f^{'}(x)$값을 더하고 뺀 $x \pm f^{'}(x)$을 계산해주면 됩니다.
총 4가지 경우가 나올 수 있습니다.
1) $f^{'}(x) > 0$ (상승함수)이면서 $x$에 덧셈
미분값이 양수이기 때문에 $x + f^{'}(x) > x$는 오른쪽으로 이동하면서 함수값 증가

2) $f^{'}(x) > 0$ (상승함수)이면서 $x$에 뺄셈
미분값이 양수이기 때문에 $x - f^{'}(x) < x$는 왼쪽으로 이동하면서 함수값 감소
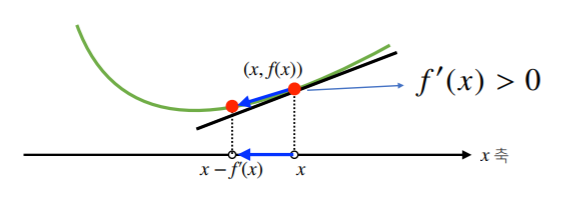
3) $f^{'}(x) < 0$ (하강함수)이면서 $x$에 덧셈
미분값이 음수이기 때문에 $x + f^{'}(x) < x$는 왼쪽으로 이동하면서 함수값 증가

4) $f^{'}(x) < 0$ (하강함수)이면서 $x$에 뺄셈
미분값이 음수이기 때문에 $x - f^{'}(x) > x$는 오른쪽으로 이동하면서 함수값 감소

위의 4가지 경우를 보면서 공통점이 있습니다.
미분 $f^{'}(x)$의 양수 음수에 상관없이 미분 값을 더하면 함수값이 증가하고, 미분값을 빼면 함수값이 감소합니다.
즉,
- 미분값을 더하면 경사상승법(gradient ascent)라고 하며 함수의 극대값의 위치를 구할 때 사용합니다.
반대로,
- 미분 값을 빼면 경사하강법(gradient descent)라고 하며 함수의 극소값의 위치를 구할 때 사용합니다.
경사상승/경사하강법은 사람이 직접 계산하는 미분 문제에서는 사용하지 못하지만, 컴퓨터에서 사용할 때 for loop를 사용해서 극소/극대 값을 찾아갈 수 있으므로 머신러닝 분야에서 많이 사용하는 방법입니다.
하지만 경사상승/경사하강 방법은미분 값이 0일 경우 더 이상 업데이트가 안돼서 굴곡이 심한 다차원 함수 그래프에서 극소값을 찾지 못하고 끝나버리는 경우도 있습니다. 이러한 문제를 해결하기 위해 머신러닝에서는 경사상승/경사하강법을 변형해서 사용하며 아래에서 다시 설명하겠습니다.
Python으로 경사하강법 의사 코드는 아래와 같습니다.
func_gradient는 미분 계산을 나타내며, init_point는 시작점, lr_rate는 (미분을 통해 업데이트하는 속도를 조절하는) 학습률, epsilon은 (미분이 정확이 0이 되는 것이 불가능하므로) 종료시키는 기준입니다.
lr_rate와 epsilon에 따라 극소값에 도달하는 속도가 달라지기 때문에 lr_rate와 epsilon를 적절한 값으로 입력해야 합니다.
val = init_point
diff, _ = func_gradient(fun, init_point) # 미분 계산
while np.abs(diff) > epsilon: # diff의 절대값이 eps보다 작아지면 out
val = val - lr_rate * diff
diff, _ = func_gradient(fun, val)
함수 $f(x) = x^{2} + 2x + 3$ 일 때 경사하강법으로 최소점을 찾는 코드입니다.
최소점이 (-1, 2)의 근사치로 수렴하는 것을 알 수 있습니다.
import sympy as sym
import numpy as np
from sympy.abc import x
def func(val):
fun = sym.poly(x**2 + 2*x +3)
return fun.subs(x, val), fun
def func_gradient(fun, val):
_, function = fun(val)
diff = sym.diff(function, x)
return diff.subs(x, val), diff
def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
cnt=0
val = init_point
diff, _ = func_gradient(fun, init_point)
while np.abs(diff) > epsilon:
val = val - lr_rate * diff
diff, _ = func_gradient(fun, val)
cnt+=1
print("함수: {}, 연산횟수 : {}, 최소점 : ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))>>> gradient_descent(fun=func, init_point=np.random.uniform(-2,2))
함수: Poly(x**2 + 2*x + 3, x, domain='ZZ'), 연산횟수 : 618, 최소점 : (-0.999995000368599, 2.00000000002500)
3️⃣ 편미분(Partial differentiation)
하나의 변수들로 함수가 존재할 수도 있지만, 여러 변수들로 함수가 존재할 수 있습니다.
이러한 함수를 다변수 함수라고 하는데 이 함수를 미분할 때는 편미분(parital differentiation)을 사용합니다.
즉, 여러 변수들 중 하나의 변수로 미분하는 것을 뜻합니다.
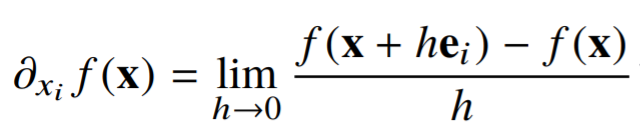
그래서 편미분은 하나의 변수를 설정해주어야 하는데요.
위의 수식의 경우 $x_{i}$의 변수로 미분하고, 다른 변수들은 모두 상수로 취급해야 합니다.
여기서 $e_{i}$는 i번째 값만 1이고 나머지는 0인 단위 벡터를 의미합니다. $e_{i}$를 사용하면 i번째 구성성분 변화율만 계산이 가능합니다.
Python 코드를 보면 $x$와 $y$로 구성된 다변수 함수를 볼 수 있습니다.
아래 코드는 $x$로 편미분 하므로 $y$는 상수로 취급해서 계산합니다.
import sympy as sym
from sympy.abc import x, y
>>> sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y), x)
2𝑥+2𝑦−sin(𝑥+2𝑦)
이렇게 각 변수 별로 편미분을 계산을 할 수 있는데 이 집합을 그레디언트(gradient) 벡터라고 합니다.

등호 왼쪽에 있는 $\nabla f$는 nabla라고 읽습니다.
등호 오른쪽에 있는 값들은 $x_{1}, x_{2}, x_{3}..x_{d}$의 변수들로 미분한 함수입니다.

아래 그림처럼 $f(x,y) = x^{2} + 2y^{2}$이라는 함수가 있다면 $\nabla f$는 $(2x, 4y)$입니다.
(여기서 $2x$는 $x$로 $f(x,y)$를 편미분한 함수, $4y$는 $y$로 $f(x,y)$를 편미분한 함수)
눈여겨봐야 할 것은 $-\nabla f$인데요.
$-\nabla f$는 극소점으로 이동하는 함수들의 집합이라는 뜻입니다.
$\nabla f$는 편미분 한 함수들의 집합이기 때문에 $-\nabla f$의 그림 중 어느 점으로 이동해도 결국 극소점에 도달할 수 있습니다.

Python을 사용해서 $f(x,y) = x^{2} + 2y^{2}$의 극소값을 구할 수 있습니다.
func_gradient는 미분 계산을 나타내며, init_point는 시작점, lr_rate는 (미분을 통해 업데이트하는 속도를 조절하는) 학습률, epsilon은 (미분이 정확이 0이 되는 것이 불가능하므로) 종료시키는 기준입니다.
lr_rate와 epsilon에 따라 극소값에 도달하는 속도가 달라지기 때문에 lr_rate와 epsilon를 적절한 값으로 입력해야 합니다.
위의 코드와 다른 점은 종료 조건(np.linalg.norm(diff))은 절대값 대신 노름(norm)을 사용했는데 벡터는 여러 개의 값들로 구성되어있기 때문에 값들의 평균을 epsilon과 비교합니다.
val = init_point
diff, _ = func_gradient(fun, val)
while np.linalg.norm(diff) > epsilon: # 벡터에서는 절대값 대신 노름(norm)을 사용합니다.
val = val - lr_rate * diff
diff, _ = func_gradient(fun, val)
전체 코드는 아래와 같습니다.
import sympy as sym
import numpy as np
from sympy.abc import x, y
def eval_(fun, val):
val_x, val_y = val
func_eval = fun.subs(x, val_x).subs(y, val_y) # subs(x, val_x)는 x에 val_x를 넣어줌(변수, 상수 모두 가능)
return func_eval
def func_multi(val):
x_, y_ = val
func = sym.poly(x**2 + 2*y**2)
return eval_(func, [x_, y_]), func
def func_gradient(fun, val):
x_, y_ = val
_, function = fun(val)
diff_x = sym.diff(function, x)
diff_y = sym.diff(function, y)
grad_vec = np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype=float)
return grad_vec, [diff_x, diff_y]
def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
cnt=0
val = init_point
diff, _ = func_gradient(fun, val)
while np.linalg.norm(diff) > epsilon:
val = val - lr_rate * diff
diff, _ = func_gradient(fun, val)
cnt+=1
print("함수: {}, 연산횟수 : {}, 최소점 : ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))
pt = [np.random.uniform(-2, 2), np.random.uniform(-2,2)]
>>> gradient_descent(fun=func_multi, init_point=pt)
함수: Poly(x**2 + 2*y**2, x, y, domain='ZZ'), 연산횟수 : 423, 최소점 : ([-4.95993065e-06 -7.73031330e-10], 2.46009132149679E-11)
4️⃣ 선형회귀분석 (using 경사하강법)

선형회귀분석은 데이터들을 선형모델(linear model = 선)로 해석하는 방법입니다.
여러 데이터들(점)에게서 최대한 가까운 $X\beta$라는 선을 찾는 것을 말합니다.
다만, 아래 그림과 같이 $X\beta$에 일치하는 정확한 $y$값을 구하는 것은 불가능하므로 ($X\beta \neq y$)
$\hat{y}$을 사용해서 $X\beta$와 일치하는 $\hat{y}$ 벡터를 만들어줍니다. ($X\beta = \hat{y}$)

그렇다면 여기서 중요한 부분은 $\hat{y}$를 구하는 것인데 $y-\hat{y}$의 차이가 최소화되는 값으로 구해야 합니다.
$y-\hat{y}$의 최소값을 구한다는 의미는 최소화된 $\beta$를 구해야 한다는 의미이므로
경사하강법에서 선형회귀를 구한다는 의미는 $\nabla _\beta ||y - X\beta||_2$라고 할 수 있습니다.
(여기 $y-\hat{y}$에서 $\hat{y} = X\beta$이므로 $\hat{y}$을 $X\beta$로 치환)
($||~||_2$는 $L_2$노름이며 $X$, $\beta$, $y$ 모두 벡터이므로 $L_2$노름을 사용)
따라서 경사하강법 $\nabla _\beta ||y - X\beta||_2$은 아래와 같이 표현될 수 있습니다.
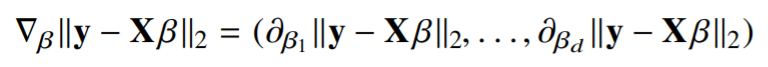
여기서 편미분 하나를 가지고 오면 아래 수식과 같이 표현됩니다.
(선형회귀에서 사용되는 $L_2$노름은 정확히 말하면 RMSE(Root Mean Squared Error) 개념으로 $L_2$노름 정의와 유사하지만 데이터 개수만큼 나눠주어야 합니다. 따라서 식에서 $1/n$으로 나눈 후에 루트로 나눠주게 됩니다.)
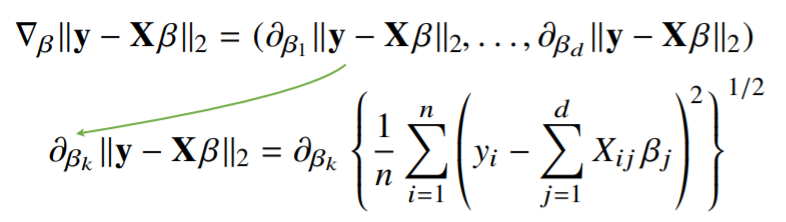
저 식을 정리해서 쓰면 아래 수식과 같이 표현됩니다.
(여기서 $X^{T}_k$는 행렬 $X$의 $k$번째 열(column) 벡터를 전치시킨 것)
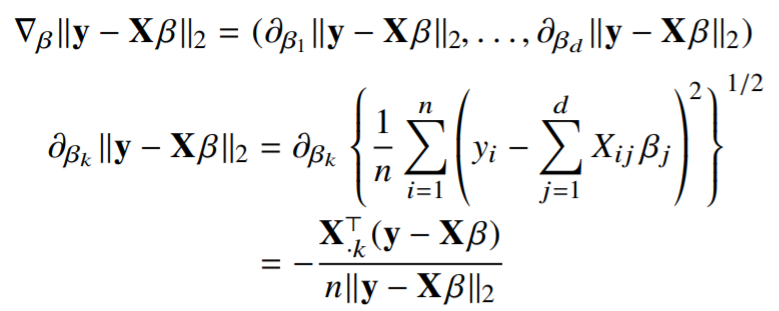
따라서 각각의 편미분을 정리해보면 아래 수식과 같습니다.
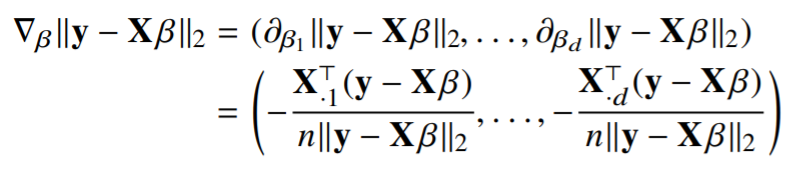
$X^{T}_1, X^{T}_2, X^{T}_3 .... X^{T}_d$는 $X^{T}$(전치행렬)로 합칠 수 있습니다.

즉, 최소화된 $\beta$를 구하는 경사하강법 알고리즘은 다음과 같습니다.
(여기서 $\lambda$는 학습률이며, 학습률에 따라 하강속도를 조절할 수 있습니다.)
(하강법이기 때문에 마이너스(-) 부호가 붙습니다.)

이 값을 위에서 구한 식으로 변경하는 아래 수식과 같습니다.
(마이너스(-)부호가 플러스(+)부호로 변경!!)
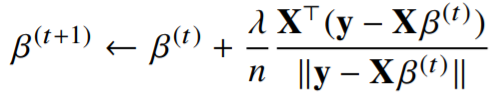
✅ $||y - X\beta||_2$ 대신 $||y - X\beta||^{2}_2$ 을 사용하면 식이 간단해집니다.
($||y - X\beta||_2$의 제곱을 사용해도 같은 극소값으로 수렴합니다.)

$||y - X\beta||^{2}_2$는 아래와 같이 사용할 수 있습니다.

Python을 사용해서 $||y - X\beta||^{2}_2$ 방식의 선형회귀 알고리즘을 구현할 수 있습니다.
여기서 error는 $||y - X\beta^{(t)}||$를 나타내고 lr는 $\lambda$를 나타냅니다.
(아래 코드에서 따로 $2\lambda/n$을 넣지 않은 이유는 상수이므로 $\lambda$값으로 조정이 가능합니다.)
for t in range(T):
error = y - X_ @ beta_gd
grad = -np.transpose(X_) @ error
beta_gd = beta_gd - lr * grad
전체 코드는 아래와 같습니다. (여기서 lr = 0.01, $2\lambda/n$ 포함)
import sympy as sym
import numpy as np
from sympy.abc import x, y
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3
beta_gd = [10.1, 15.1, -6.5] # beta_gd는 어떤 값이라도 횟수가 충분하다면 수렴
X_ = np.array([np.append(x, [1]) for x in X]) # 배열 shape가 맞지 않기 때문에 마지막 열에 1을 추가
for t in range(5000):
error = y - X_ @ beta_gd
# error = error / np.linalg.norm(error)
grad = -np.transpose(X_) @ error
beta_gd = beta_gd - 0.01 * grad
>>> print(beta_gd)
[1.00000367 1.99999949 2.99999516] # [1, 2, 3]이 정답, 유사하다는 것을 알 수 있음
중요한 점은 T(학습횟수)를 충분히 돌리지 않으면 값이 제대로 나오지 않을 수 있습니다.
만약, for문을 100번만 돌렸을 경우 값이 제대로 수렴하지 않습니다.
>>> for t in range(100):
[ 3.41314549 4.63604548 -6.69249764]하지만 적절한 학습률과 학습 횟수를 선택했을 때는 수렴이 보장됩니다.
경사하강법은 미분이 가능하고 볼록(convex)한 함수에 대해선
적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장됩니다.
5️⃣ 확률적 경사하강법 (Stochastic gradient descent)
하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있습니다.

또는 볼록한 부분이 있더라도 그 부분이 전체 함수의 극소값이 아닐 수 있습니다.
(딥러닝에서는 볼록한 부분이 여러 곳이 있을 수 있으므로 극소값이 아닐 수 있습니다.)
이러한 경우를 위해 확률적 경사하강법(stochastic gradient descent)이 존재합니다.
확률적 경사하강법이란 모든 데이터를 사용해서 극소값을 찾는 것이 아닌 데이터를 한 개 또는 일부 활용하여 경사하강법을 수행하는 방법입니다.

확률적 경사하강법은 SGD라는 약자를 가지며,
- 데이터 한개만 사용할 때 : SGD
- 데이터 일부를 사용할 때 : mini batch SGD
라고 불립니다.
SGD의 장점은 데이터의 일부만 사용하기 때문에 $O(d^{2}n)$의 시간복잡도에서 $O(d^{2}b)$로 줄일 수 있는 장점이 있습니다. (n은 전체 데이터, b는 일부 데이터)

확률적 경사하강법은 전체 데이터를 아래와 같이 표시합니다.

전체 데이터를 가진 목적식의 그레디언트 벡터는 아래와 같이 표시합니다.
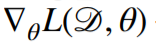
일부 데이터(mini batch)를 가진 목적식의 그레디언트 벡터는 아래와 같이 표시합니다.
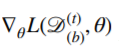
따라서 확률적 경사하강법에서는 $\theta^{(t)}$에서의 그레디언트 벡터와 $\theta^{(t+1)}$에서의 그레디언트 벡터가 다르게 됩니다. 계속해서 다른 데이터들로 구성된 목적식을 만들어주기 때문이죠.

따라서 SGD의 장점은 그레디언트를 계속해서 산출해내기 때문에 $\theta^{(t)}$에서 극소값이라고 생각했던 위치에서 $\theta^{(t+1)}$의 그레디언트를 산출했을 때 극소값이 아니라면 Local minimum을 탈출할 수 있게 됩니다.
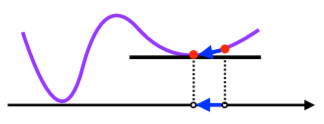
예를 들어, 아래와 같은 함수가 존재할 때, 경사하강법을 사용하게 되면 최소값으로 수렴하게 됩니다.
문제는 볼록(convex)한 부분이 두 부분인데 운이 좋으면 왼쪽 최소값으로 값이 수렴해서 극소값을 찾을 수 있지만, 운이 나쁘면 오른쪽 최소값에 값이 수렴할 수도 있습니다. (경사하강법은 기울기가 0이 되면 멈추게 됩니다.)
이 것을 Local minium라고 합니다.

하지만 SGD는 $\theta^{(t)}$에서 $\theta^{(t+1)}$로 이동할 때마다 새로운 그레디언트 벡터를 산출하므로 오른쪽 최소값으로 값이 수렴해도 높은 확률로 Local minimum을 탈출할 수 있게 됩니다. 극소값이라고 생각한 해당 위치에서 새로운 그레디언트를 구했을 때 극소값이 아니라면 말이죠.
따라서 확률적 경사하강법은 데이터 일부를 사용해서 여러 번의 그레디언트 벡터를 새로 만들기 때문에 일정하게 하강하지 않습니다.
하지만 속도는 데이터의 개수 선택만 적절하다면 경사하강법보다 효율적이라고 말할 수 있습니다. 훨씬 적은 데이터를 사용하기 때문에 계산이 빨라집니다. (그렇지만 SGD에서 batch사이즈를 너무 작게 잡으면 경사하강법 알고리즘보다 느리게 수렴할 수 있습니다.)

또한, 확률적 경사하강법을 사용하는 이유는 데이터가 너무 많아서 메모리에 올리지 못하기 때문입니다.
영상 처리를 할 때 수많은 데이터를 처리를 하게 되고 아래 그림과 같이 메모리에 올리지 못하는 불상사가 발생합니다.

하지만 확률적 경사하강법을 사용하면 데이터 일부만 사용하기 때문에 훨씬 수월하게 딥러닝을 수행할 수 있습니다.

'부스트캠프 AI 테크 U stage > 이론' 카테고리의 다른 글
| [08-1] 신경망(neural network) (0) | 2021.01.27 |
|---|---|
| [08] Python pandas (1) (1) | 2021.01.27 |
| [06-1] 벡터와 행렬 with Python Numpy (0) | 2021.01.25 |
| [06] Python numpy (1) | 2021.01.25 |
| [05] Python Exception/File/Log /data Handling (0) | 2021.01.22 |




