| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- namedtuple
- subplot
- pivot table
- boolean & fancy index
- 카테고리분포 MLE
- scatter
- unstack
- BOXPLOT
- 표집분포
- type hints
- Python
- 부스트캠프 AI테크
- groupby
- 딥러닝
- Comparisons
- seaborn
- Numpy
- Operation function
- ndarray
- 가능도
- Numpy data I/O
- Python 특징
- python 문법
- 정규분포 MLE
- Python 유래
- 최대가능도 추정법
- linalg
- dtype
- VSCode
- Array operations
- Today
- Total
또르르's 개발 Story
[08-1] 신경망(neural network) 본문
오늘은 신경망을 수학적으로 분해해보는 시간을 가졌습니다.
1️⃣ 신경망(neural network)
신경망(neural network)은 기계학습에서 생물학의 신경망에서 영감을 얻은 통계학적 학습 알고리즘입니다.
신경망은 수많은 데이터를 분석해서 만들어지는 학습 알고리즘이며, 따라서 선형 모델로 만들기에는 너무 많은 예외와 변수가 존재해 무리가 있습니다.
따라서 신경망은 비선형모델이며 아래 그림과 같이 행렬곱으로 이루어집니다.
신경망의 구성요소는 아래와 같습니다.
- O 행렬 : Output 행렬
- X 행렬 : Input(데이터) 행렬
- W 행렬 : 가중치 행렬
- b 벡터 : 절편 (bias) 벡터 (각 행들이 같은 값을 가지고 있음)

즉, 각 행벡터 $o_{i}$는 데이터 $X_{i}$와 가중치 행렬 $W$ 사이의 행렬곱과 절편 $b$ 벡터의 합으로 이루어집니다.
$$O = XW+b$$
따라서 데이터를 input 해주는 $X$ 행렬의 값이 바뀌면 결과값 $O$의 결과도 바뀌게 됩니다.
아래 그림은 행렬 수식을 그래프로 표현한 모습입니다.
여기서 $x_{1}, x_{2}, x_{3} ... x_{d}$는 $X$ 행렬을 나타내고, $o_{1}, o_{2} ..... o_{p}$는 $O$ 행렬을 나타냅니다.
그리고 $X$에서 $O$로 이어지는 화살표들은 가중치 행렬 $W$를 나타냅니다. (화살표 개수 $p * d$)

이렇게 나온 $O$ 행렬의 값들은 softmax 함수를 거치게 됩니다.
2️⃣ 소프트맥스(Softmax) 연산
소프트맥스(softmax) 함수는 $O = XW+b$ 계산에서 나온 $O$의 출력을 확률로 해석할 수 있게 변환해주는 연산입니다. 즉, 소프트맥스 함수는 $XW + b$ 벡터를 확률 벡터로 변환시켜줍니다.
소프트맥스 함수의 수식은 아래와 같이 표현됩니다. (exp = 지수)

수식이 비교적 간단하기 떄문에 Python 코드로 만들면 아래와 같이 구현할 수 있습니다.
(softmax는 현재의 지수값 / 전체 지수값으로 나눈 값)
def softmax(vec):
denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True)) # np.max를 뺀 이유는 아래 참조
numerator = np.sum(denumerator, axis=-1, keepdims=True)
val = denumerator / numerator # 현재 지수값 / 전체 지수값
return val랜덤 벡터를 넣고 돌리면 아래와 같이 확률 벡터로 표시됩니다.
vec = np.array([[1, 2, 0], [-1, 0, 1], [-10, 0, 10]])
>>> softmax(vec)
array([[2.44728471e-01, 6.65240956e-01, 9.00305732e-02],
[9.00305732e-02, 2.44728471e-01, 6.65240956e-01],
[2.06106005e-09, 4.53978686e-05, 9.99954600e-01]])✅ softmax 함수의 denumerator를 구할 때 np.max를 뺀 이유?
소프트맥스 함수는 지수를 사용하기 때문에 값이 너무 커져 overflow가 발생할 수 있습니다.
따라서 지수의 양수 부분이 아닌 지수의 음수 부분을 사용합니다.
아래 그림과 같이 지수 함수가 양수일 때는 무한대로 뻗어나가지만, 지수함수가 음수 일 때는 0에 근사하기 때문에 overflow가 발생할 일이 없습니다.

따라서 input vector에서 max값을 기준으로 input vector값을 빼주면 모두 마이너스 값이 나오게 되고, 이 값을 exp 시키면 아래 코드와 같이 0에 근사한 값들이 나오게 됩니다.
[[3.67879441e-01 1.00000000e+00 1.35335283e-01]
[1.35335283e-01 3.67879441e-01 1.00000000e+00]
[2.06115362e-09 4.53999298e-05 1.00000000e+00]]이 값들을 (현재의 지수값 / 전체 지수값)으로 계산하면 지수의 양수 부분을 사용한 확률 벡터와 똑같은 값이 나오게 됩니다.
소프트맥스 함수는 분류 문제를 풀 때 선형 모델과 함께 쓰이며, 분류를 예측할 때 사용됩니다.
또한, 예측을 할 때는 원-핫(one-hot) 벡터를 사용하지 않는데 이유는 최대값을 가진 주소만 1로 출력하고 나머지는 0으로 출력하기 때문에 알맞지 않습니다. (추론을 할 때는 원-핫(one-hot) 벡터를 사용합니다.)
3️⃣ 활성 함수 (Activation function)
분류 문제는 softmax 함수를 사용해서 원래 선형 모델로 나온 출력 값에다가 softmax 함수를 씌어 사용했습니다.
softmax 함수를 씌우면 원래 선형 모델의 결과물에서 원하고자 하는 의도로 바꿔서 해석할 수가 있습니다.
이와 비슷하게 활성 함수를 사용해서 비선형 모델을 분석이 가능합니다.
활성 함수는 행렬곱을 사용하지 않고 선형 모델로 나온 output의 각각의 원소에다가 적용하는 함수입니다.
softmax 함수와 다른 점은,
softmax 함수는 모든 output에 대해 값을 고려해서 출력을 하지만, 활성 함수는 다른 주소에 있는 output은 고려하지 않고 자신의 주소에 있는 output만 고려합니다. 그렇기 때문에 활성 함수는 벡터를 받지 않고 하나의 원소(실수 값)만 받게 됩니다. (아래 그림과 같이 $z_{1}$은 $\sigma(z_{1})$에만, $z_{2}$은 $\sigma(z_{2})$에만 영향을 미칩니다.)


따라서 활성 함수는 실수 값을 input으로 받아서 실수값을 output 하는 함수입니다.
벡터를 input으로 받지 않고 실수 값만 input으로 받기 때문에 딥러닝에서는 선형 모델로 출력된 값을 비선형 모델에 적용이 가능하게 됩니다. (활성 함수를 사용하지 않으면 딥러닝은 선형 모형과 차이가 없습니다.)
이렇게 변형을 시킨 활성 함수의 벡터($\sigma(z_{n})$들의 집합)는 Hidden vector이라고 부르며, 뉴런이라고 합니다.

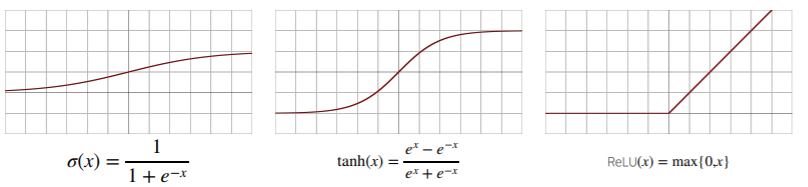
활성 함수는 대표적으로 3가지가 존재합니다.
시그모이드(sigmoid) 함수($\sigma(x)$)나 tanh 함수($tanh(x)$)는 전통적으로 많이 쓰이던 함수이지만 딥러닝에서는 ReLU 함수가 많이 사용되고 있습니다.
활성함수 벡터 $H$는 신경망 안에 여러 개 존재할 수 있으며, 벡터 $H$의 값을 다시 선형 모델($WX+b$)의 input으로 넣을 수 있습니다. 이러한 경우 가중치 벡터가 2개가 생기며 ($W^{(2)}, W^{(1)}$), 2층(2-layers) 신경망이라고 말합니다.

이렇게 여러 겹의 layer를 계속해서 쌓아갈 수 있으며, 여러 층(multi-layer)으로 구성된 신경망은 다층(multi-layer) 퍼셉트론(MLP)라고 부릅니다.
아래 그림은 $L$층으로 구성된 MLP이며, $W^{(L)}, ...... , W^{(1)}$ 가중치 행렬로 이루어져 있습니다.
이렇게 Layer가 많아지게 되면 중간에 활성 함수를 무조건 사용해야 합니다.

✅ 왜 층을 여러 개를 쌓나요?
이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있습니다.
하지만 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능합니다.
층이 얇게 되면 한 층에서 필요한 뉴런의 숫자가 기하급수적으로 늘어나서 넓은(wide) 신경망이 되어야 합니다.

4️⃣ 순전파(forward propagation) / 역전파(backpropagation)
1) 순전파(forward propagation)
순전파는 $\ell = 1, ...... , L$ 까지 순차적인 신경망 계산을 뜻합니다.
실제 분류나 추론 등을 할 때 신경망이 지금까지 학습한 결과를 산출해내는 과정입니다.

2) 역전파(backpropagation) : 딥러닝 학습원리
역전파는 결과값을 사용해 $L, ....., 1$ 역순으로 신경망 계산하는 것을 뜻합니다.
즉, 출력층에서 입력층 방향으로 이동하면서 가중치를 업데이트하는 것을 말합니다.

역전파에서는 경사하강법 그레디언트 벡터(미분)를 사용하며 연쇄법칙을 통해 그레디언트 벡트를 전달합니다.

여기서 연쇄법칙은 합성함수의 미분 공식입니다.
예시로, 아래 수식들과 같이 $z = (x+y)^{2}$을 $w=x+y$라고 했을 때 $z = w^{2}$으로 치환이 가능합니다. $\frac{\partial z}{\partial w} = 2w$가 나오고, $\frac{\partial w}{\partial x} = 1$로 만들 수 있게 되면서, 최종으로 $\frac{\partial z}{\partial x} = 2(x+y)$라는 값이 나오게 됩니다.

위의 연쇄법칙처럼 신경망 역전파 알고리즘에서는 상위 레이어에 있는 다변수 함수를 하위 레이어에 있는 변수로 계속해서 미분해줍니다.
2층 신경망을 역전파하면 아래와 같은 수식이 나옵니다.
($\nabla_{W^{(1)}}L$은 $\frac{\partial L}{\partial W^{(1)}_{ij}}$를 나타냅니다.)
(여기서 $\delta_{rk}$는 크로네커-델타(Kronecker delta)로 $i=j$ 면 1, $ i\neq j$ 면 0을 나타냄)

수식을 정리하면 아래와 같이 표현됩니다.

중요한 점은 역전파 알고리즘을 수행할 때 각 노드의 텐서 값($z, h, o, w$ 등)을 메모리에 기억해두어야만 역전파가 가능합니다.
따라서 각 노드의 텐서 값($z, h, o, w$ 등)은 forward를 수행할 떄 (torch에서 requires_grad=true인 경우 추적) 값들을 저장해놓습니다.
'부스트캠프 AI 테크 U stage > 이론' 카테고리의 다른 글
| [09-1] 딥러닝에 사용되는 확률론 (0) | 2021.01.28 |
|---|---|
| [09] Python pandas (2) (0) | 2021.01.28 |
| [08] Python pandas (1) (1) | 2021.01.27 |
| [07] 경사하강법 (0) | 2021.01.26 |
| [06-1] 벡터와 행렬 with Python Numpy (0) | 2021.01.25 |




